Przedmioty

KnowunityAI

Kariera

Program dla Twórców

Knowunity Pro

Otwórz aplikację

Przedmioty

Math Help

How to use AI to solve math problems (step-by-step)

By Niklas Heist•
January 10, 2026
•
10 min read

How to use AI to solve math problems step−by−stepstep-by-step

Struggling with your Maths homework?

Join the club. There is probably no other subject out there that causes as many problems as Maths. We all have been there dreading our maths homework out of fear of utter confusion.

Luckily AI and LLMs are a game changer when it comes to solving and explaining Maths. With just a few simple steps you can use modern tools like ChatGPT or Knowunity to help you not only solve but also understand your maths homework.

In this article I am going to show you with an example how ChatGPT & Knowunity can help you with your maths homework. We will go over an example once with ChatGPT, including prompting and best practices. Afterwards I am going to show you how you can use Knowunity.

Using Analysis as example

To walk through an exercise we will use the example below:

Math Problem

We are looking at a standard analysis task. We need to first build the derivative and then find the high & low points of the function f(x)=x2+4x+3f(x) = x^2+4x+3.

This is a great example since it covers the core concepts one needs to learn for analysis:

  • Building derivative functions

  • Solving formulas for x and 0

  • Finding x and y coordinates of a function

Lets jump right in and solve this example tasks with one of the common AI tools.

Solving Maths homework with ChatGPT

In this section I will walk you through the example step by step within ChatGPT.

Firstly open ChatGPT and upload a picture of your task or homework.

To do so go on the home page of the ChatGPT App, klick on the plus icon in the bottom left corner. This will open a section in the App in which you can choose between different tools like Camera, Photos and Files. Select the picture upload, then take a photo of the task. You will end up with the photo of your task uploaded to the chat.

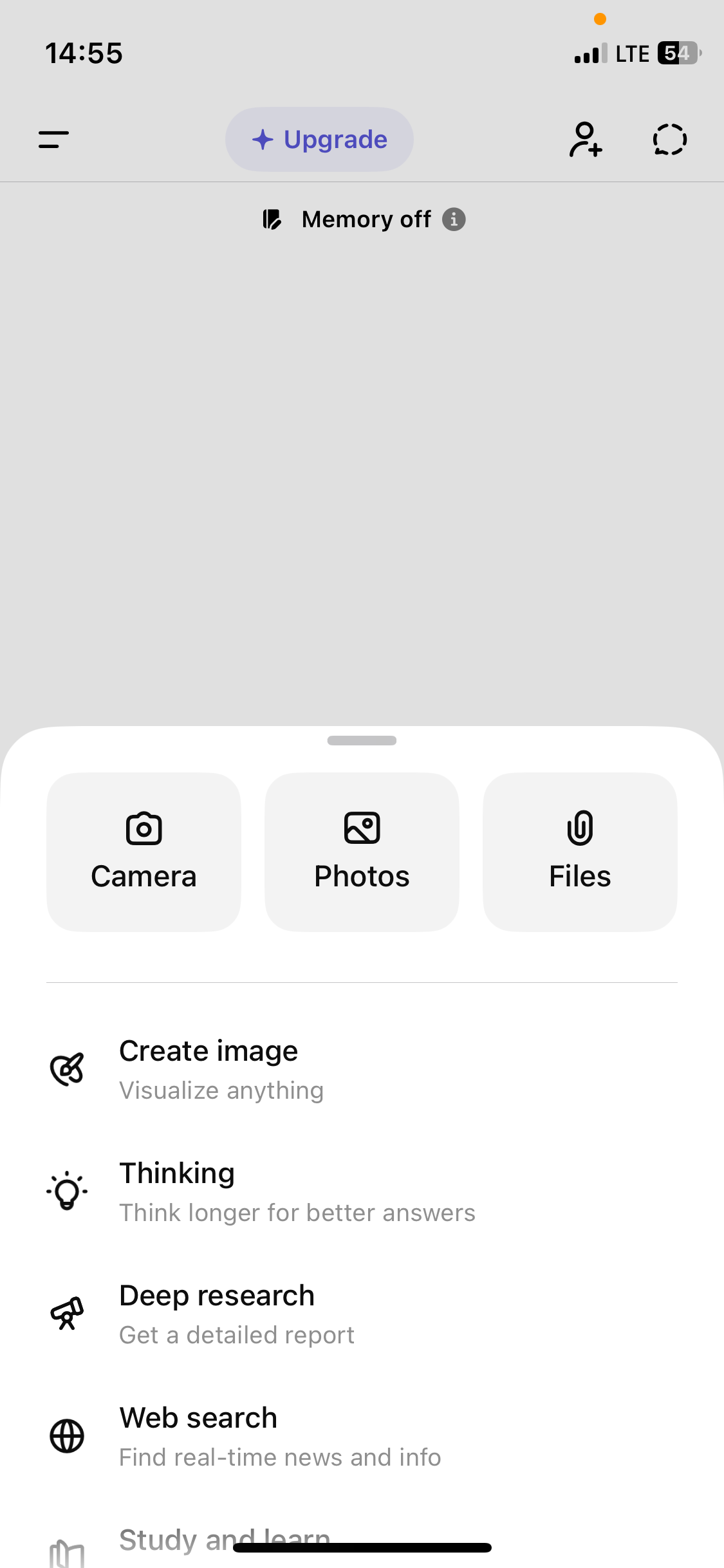
ChatGPT Upload Step 1 ChatGPT Upload Step 2 ChatGPT Upload Step 3

In the next step we need to write the prompt for the model. In the prompt we need to specify what our goal is and how we would like to receive the answer. For example we can ask ChatGPT to only solve our homework or to also explain us the step by step.

A well working prompt would be the following:


Solve the task in the image.

Show all steps (derivative, critical points, classification, etc.) of the

exercise along the way.

Explain them step by step so a student can follow.

Insert this prompt and you are basically done. ChatGPT will send you back a well formatted solution and explanation for the task.

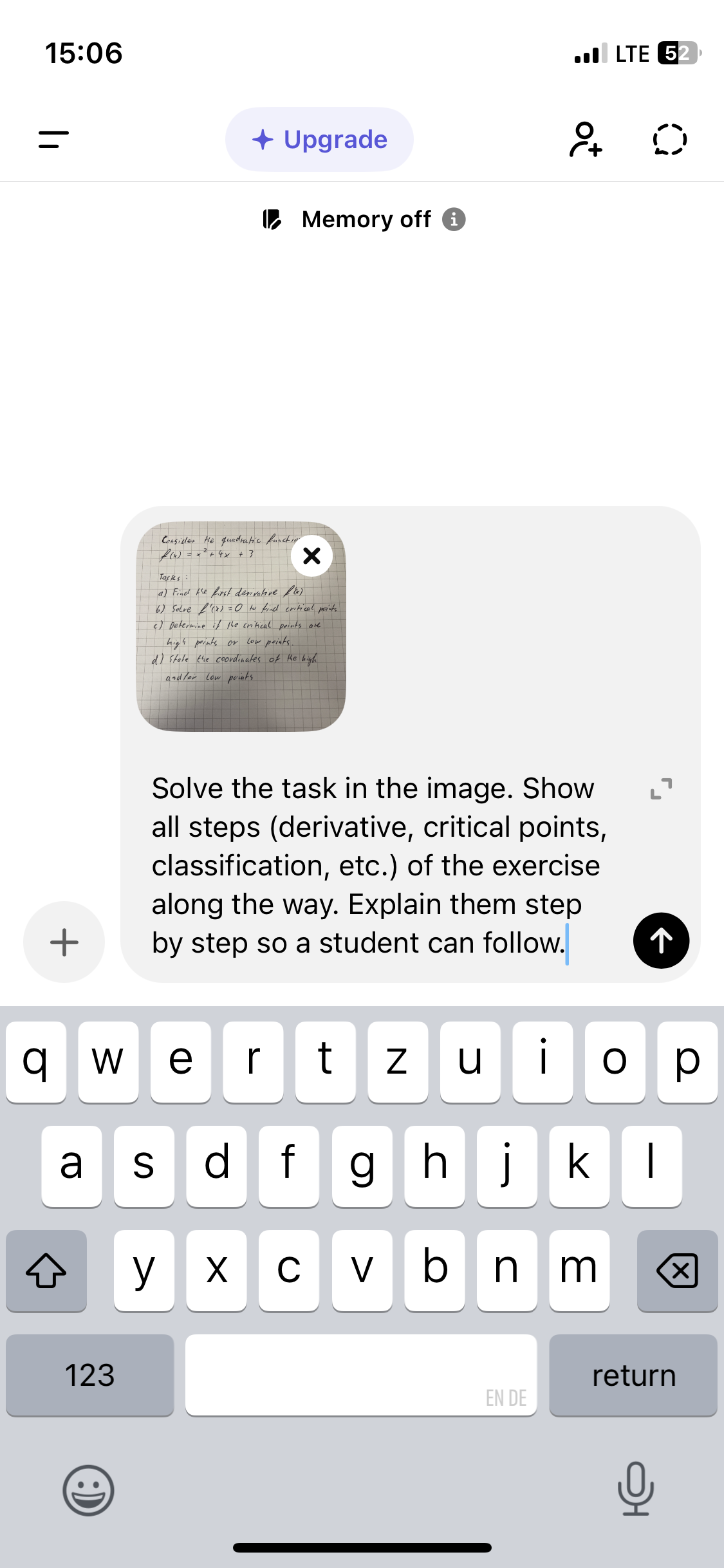
ChatGPT Response 1 ChatGPT Response 2 ChatGPT Response 3

The solution you will receive will look like the following:

 
Let's work this through step-by-step.
 
Given:
 
f(x)=x2+4x+3f(x)=x^2+4x+3
 
⸻
 
1) First derivative f'(x)
 
Differentiate term by term:
 
ddx(x2)=2x,ddx(4x)=4,ddx(3)=0.\frac{d}{dx}(x^2)=2x,\qquad \frac{d}{dx}(4x)=4,\qquad \frac{d}{dx}(3)=0.
 
So
 
f′(x)=2x+4.\boxed{f'(x)=2x+4.}
 
⸻
 
2) Critical points(solvef′(x)=0)s (solve f'(x)=0)
 
Set the derivative equal to zero:
 
2x+4=0⇒2x=−4⇒x=−2.2x+4=0 \quad\Rightarrow\quad 2x=-4 \quad\Rightarrow\quad x=-2.
 
So there is one critical point at x=-2.
 
⸻
 
3) Classify the critical point (max or min)
 
Compute the second derivative:
 
f′′(x)=ddx(2x+4)=2.f''(x)=\frac{d}{dx}(2x+4)=2.
 
Because f′′(x)=2>0f''(x)=2>0 for all x, the graph is concave up everywhere and any critical point is a local minimum (in fact the global minimum for this upward-opening parabola).
 
Therefore the critical point at x=-2 is a minimum (a low point).
 
⸻
 
4) Coordinates of the low point
 
Evaluate f at x=-2:
 
f(−2)=(−2)2+4(−2)+3=4−8+3=−1.f(-2)=(-2)^2+4(-2)+3 =4-8+3 =-1.
 
So the minimum point is at
 
(−2, −1).\boxed{(-2,\,-1).}
 
(There is no maximum point because the parabola opens upward and extends to +∞\infty as x→±\to\pm∞\infty.)
 
⸻
 
Short summary
 
• f′(x)=2x+4.f'(x)=2x+4.
 
• Critical point: x=-2.
 
• f′′(x)=2>0f''(x)=2>0 so it is a minimum.
 
• Minimum point: (-2,-1).
 
(Optional neat form: f(x)=(x+2)2−1f(x)=(x+2)^2-1, which makes the minimum (-2,-1) obvious.)
 
 

In case you have follow up questions or are not sure if you understood all concepts of the task here are some follow up prompts that you can ask the model to sharpen you understanding:

  • Can you explain the core idea behind this topic in simple words?

  • Can you explain what this result means graphically?

  • Can you re-explain the most important part again, but simpler?

  • What are common mistakes students make with this topic?

  • Give me a quick cheatsheet.

With the very quick and simple walk through above you are fully ready to tackle your Maths homework with AI.

Knowunity SchoolGPT, specialized for school & maths

At Knowunity we are constantly working on building a specialized School AI and School GPT. Of course you can also solve your Maths homework with our AI.

Within the Knowunity App getting solutions and explanations to your Math homework is even easier. To do so, first go to the home tab of the Knowunity App. On there click on the camera icon on the top left or the Scan Speech bubble in the middle to open our Homework Scanner. Choose the Solve chip within the camera wheel. From there simply snap a photo and mark the exercise you want to solve.

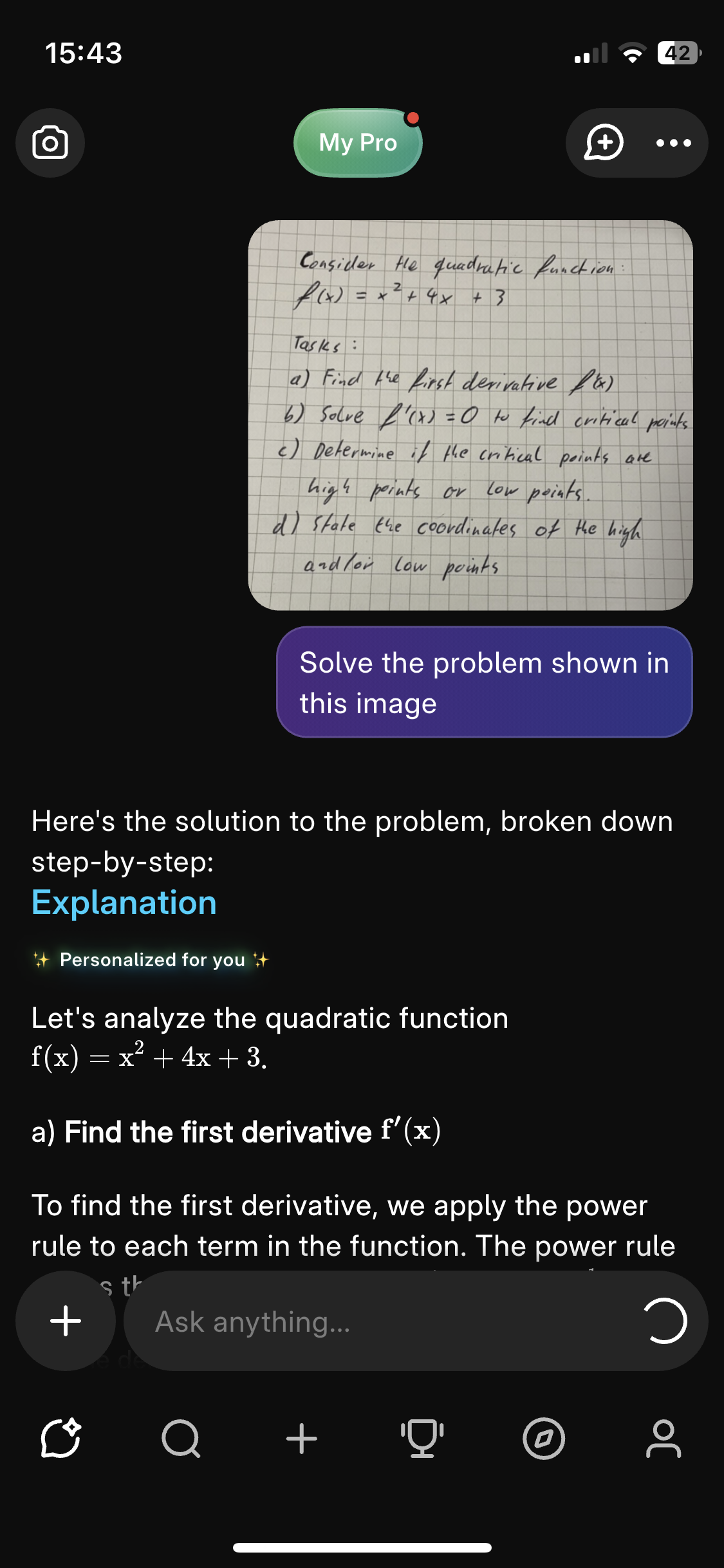
Knowunity App Step 1 Knowunity App Step 2 Knowunity App Step 3

As easy as that you will receive the solution for your homework.

Your answer will look like this:

 
Here's how to solve the problem step-by-step:
 
a) Find the first derivative f′(x)f'(x) of the function f(x)=x2+4x+3f(x) = x^2 + 4x + 3.
 
To find the derivative, we apply the power rule, which states that if f(x)=xnf(x) = x^n, then f′(x)=nxn−1f'(x) = nx^{n-1}. We also use the fact that the derivative of a constant is zero.
 
f(x)=x2+4x+3f(x) = x^2 + 4x + 3
 
f′(x)=2x+4f'(x) = 2x + 4
 
b) Solve f′(x)=0f'(x) = 0 to find the critical point(s).
 
We set the first derivative equal to zero and solve for xx:
 
2x+4=02x + 4 = 0
 
2x=−42x = -4
 
x=−2x = -2
 
So, the critical point occurs at x=−2x = -2.
 
c) Determine if the critical point is a high point (maximum) or a low point (minimum).
 
To determine whether the critical point is a maximum or minimum, we can use the second derivative test. We find the second derivative f′′(x)f''(x):
 
f′(x)=2x+4f'(x) = 2x + 4
 
f′′(x)=2f''(x) = 2
 
Since f′′(x)=2f''(x) = 2 is positive for all xx, the function is concave up everywhere. This means that the critical point at x=−2x = -2 is a local minimum (low point).
 
d) State the coordinates of the high and/or low points.
 
We know that the critical point occurs at x=−2x = -2. To find the yy-coordinate, we plug this value back into the original function f(x)f(x):
 
f(−2)=(−2)2+4(−2)+3f(-2) = (-2)^2 + 4(-2) + 3
 
f(−2)=4−8+3f(-2) = 4 - 8 + 3
 
f(−2)=−1f(-2) = -1
 
Therefore, the coordinates of the low point are (−2,−1)(-2, -1). Since the quadratic function opens upwards (because the coefficient of x2x^2 is positive), there is no high point (maximum).
 
a) f′(x)=2x+4f'(x) = 2x + 4
 
b) x=−2x = -2
 
c) Low point (minimum)
 
d) (−2,−1)(-2, -1)
 
 

The Knowunity AI will automatically suggest follow up prompts to continue the conversation and deepen your understanding.

Additionally to that you can also create quizzes and flashcards with the Knowunity App so you can continue learning if you want to. Simply ask the Ai to generate a Quiz or Flashcard set.

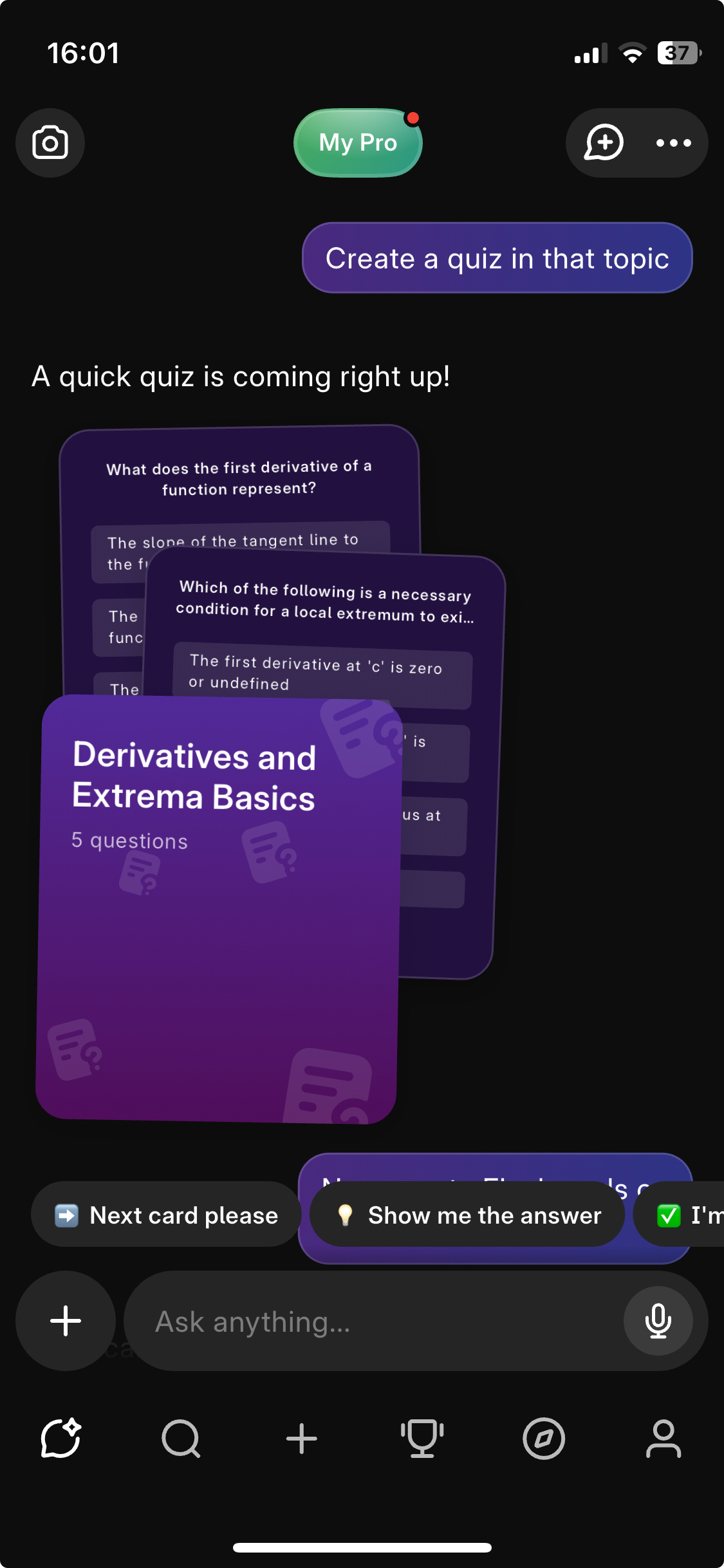
Knowunity Flashcards 1 Knowunity Flashcards 2 Knowunity Quiz 1 Knowunity Quiz 2

And thats it. Now you know how to use AI Tools like ChatGPT or Knowunity to solve and explain your math homework.

Pitfalls

Before you head off to try it out yourself please have a look at these two common mistakes when using AI for Maths:

  • Over relying on AI: Despite the high quality of the models please always recap the calculation of the AI. Try to understand how it got to the solution and verify the outcome ourself.

  • Cheating yourself: Just because your homework is done now doesn't mean you fully grasped the concept. The goal is to learn alongside the AI, not to let it replace your own thinking. To understand the topic walk through the exercise yourself.

Avoid these two mistakes in order to get the best learning outcome.

Conclusion

LLMs & AI can be incredibly useful for your math exercises and homework. If used correctly they can make your learning journey way easier and faster. Use the tools responsible, recap the exercises on your own and you will be ready to ace your exams in no time.

Master Math with AI

Get step-by-step solutions and explanations for your math homework with Knowunity's specialized AI tutor. Learn smarter, not harder.

About the Author

NH

Niklas Heist

Product Manager at Knowunity. Passionate about making learning more accessible through AI.

Related Articles

Best ChatGPT Alternatives for School
AI Tools
9 min read

Best ChatGPT Alternatives for School

ChatGPT is great, but it's not your only option. Discover the best AI tools for high school students, from research and writing to homework help and studying.

Niklas Heist
The 10 Best Prompts for School
AI for Education
6 min read

The 10 Best Prompts for School

Master AI for schoolwork with these 10 ready-to-use prompts. Learn how to write effective prompts that get you exactly what you need for homework, studying, and test prep.

Niklas Heist
How to Automatically Turn Your Notes into Flashcards with AI
Study Tools
7 min read

How to Automatically Turn Your Notes into Flashcards with AI

Stop spending hours creating flashcards manually. Learn how to use AI tools like ChatGPT and Knowunity to automatically generate effective flashcards from your notes in minutes.

Niklas Heist

Want to learn smarter?

Explore more articles, tutorials, and best practices to help you study with AI.

Browse All Articles