A comprehensive guide to gravitational forces and celestial mechanics, explaining prawo powszechnego ciążenia wyjaśnienie and orbital dynamics. The material covers Newton's law of universal gravitation, gravitational fields, and Kepler's laws of planetary motion.
- Universal gravitation describes the force between any two masses, which is proportional to their masses and inversely proportional to the square of distance
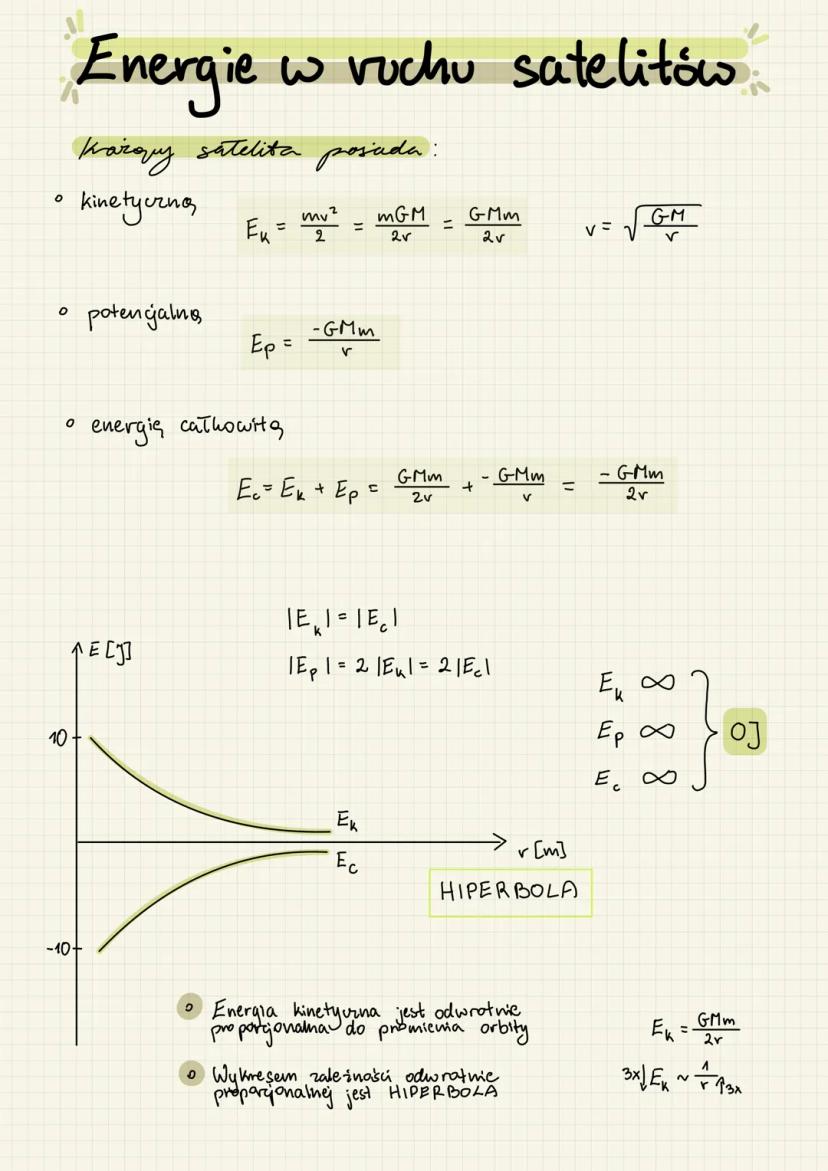
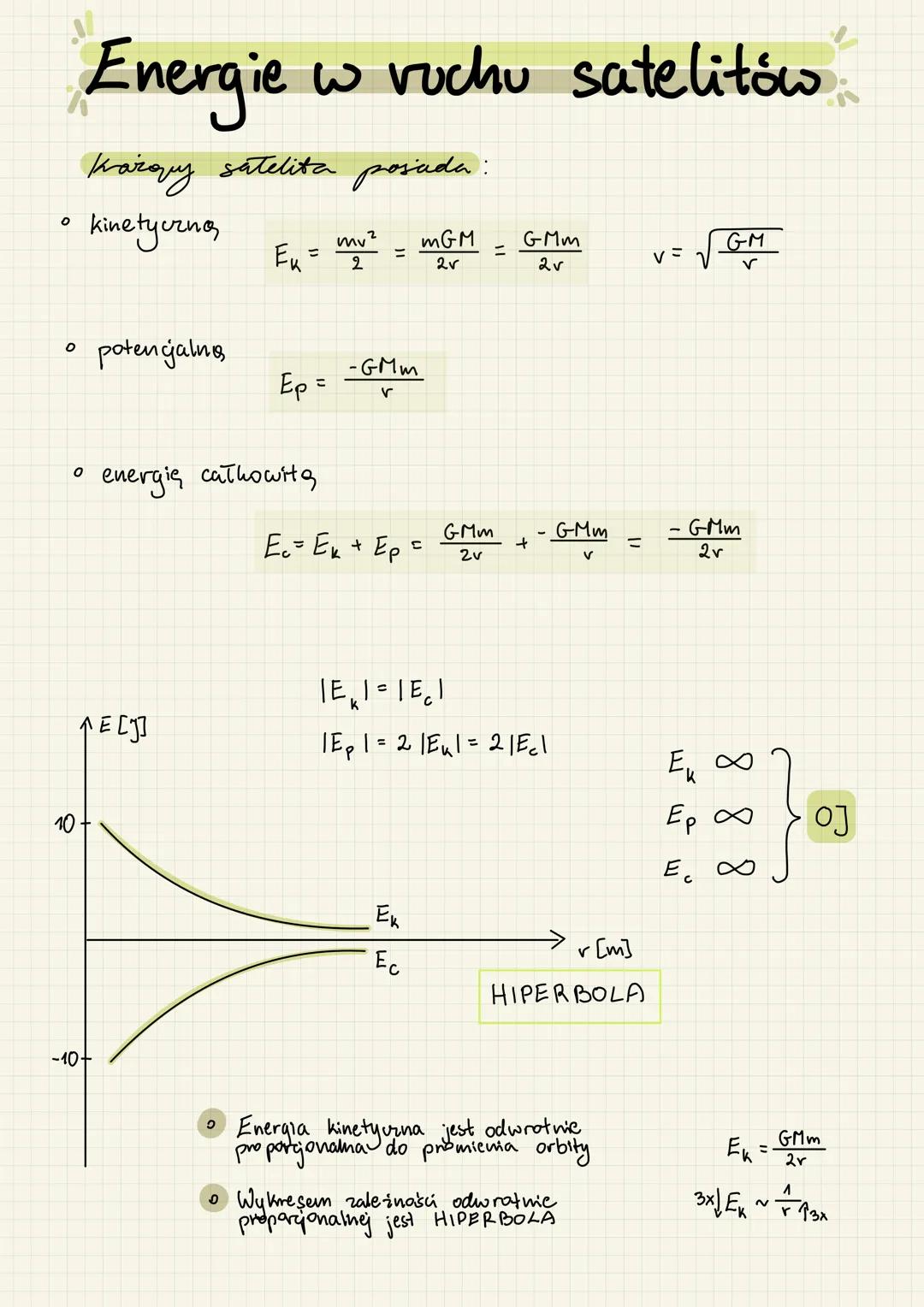
- Natężenie pola grawitacyjnego a odległość shows how gravitational field strength decreases with distance following an inverse square relationship
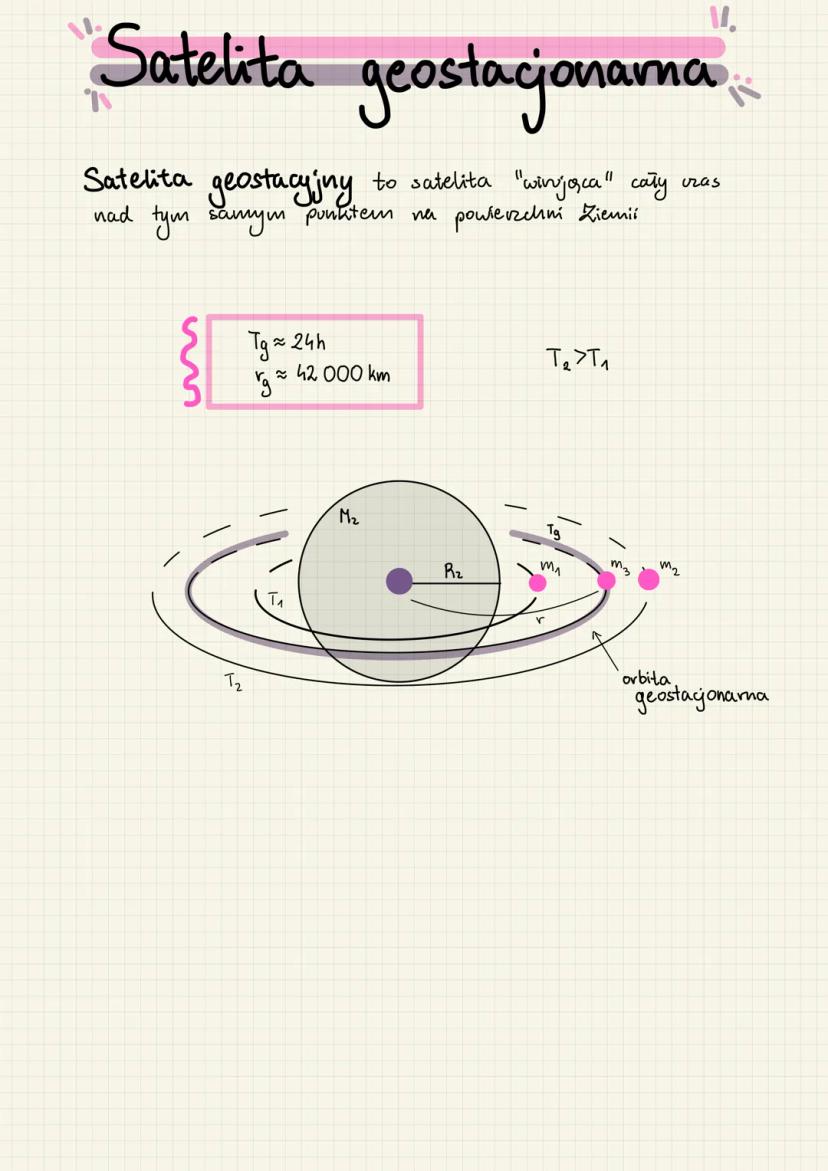
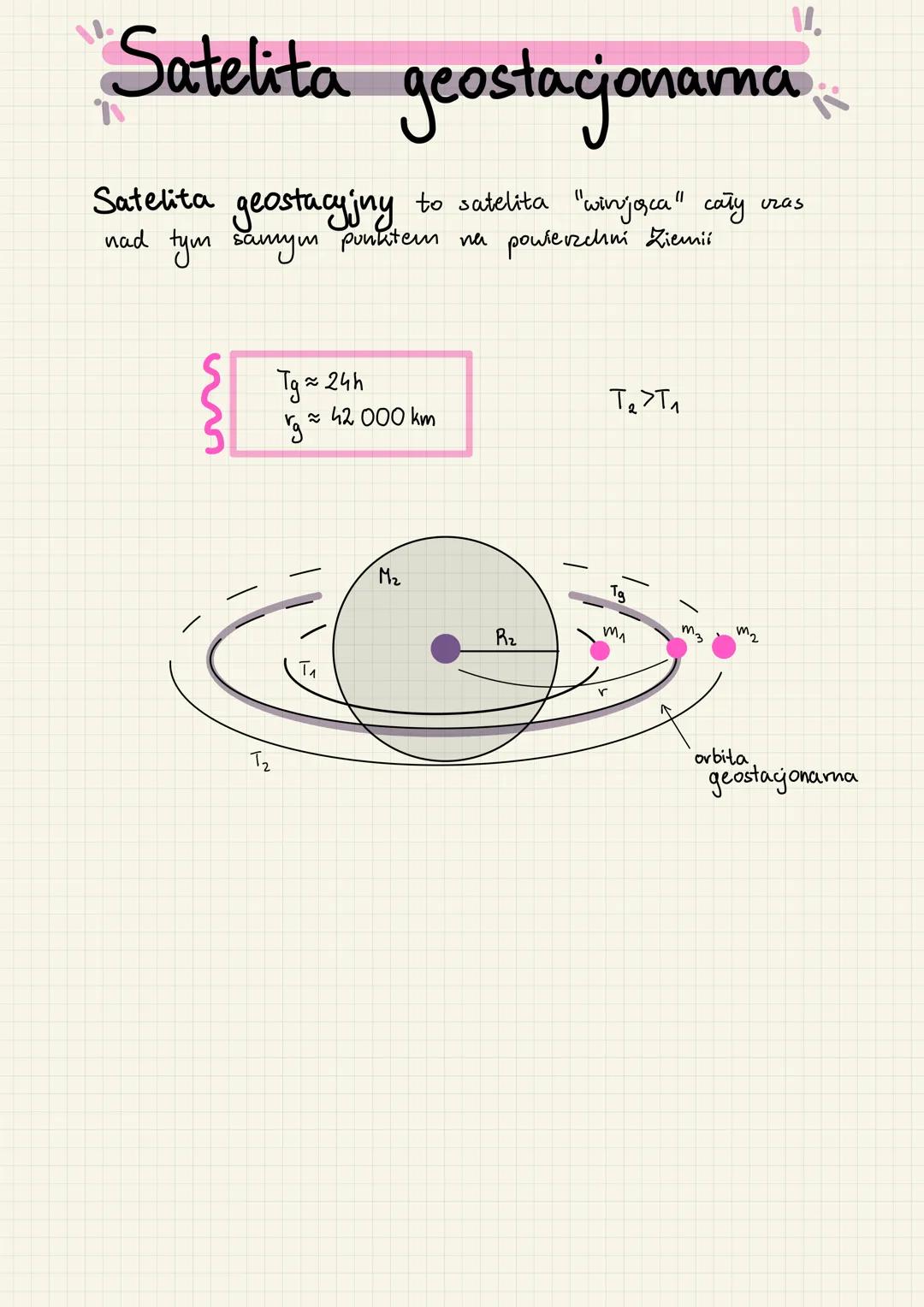
- Orbital mechanics explains satellite motion, including the special case of satelita geostacjonarny nad Ziemią which appears stationary above Earth
- The laws of conservation of energy and angular momentum govern celestial body movements
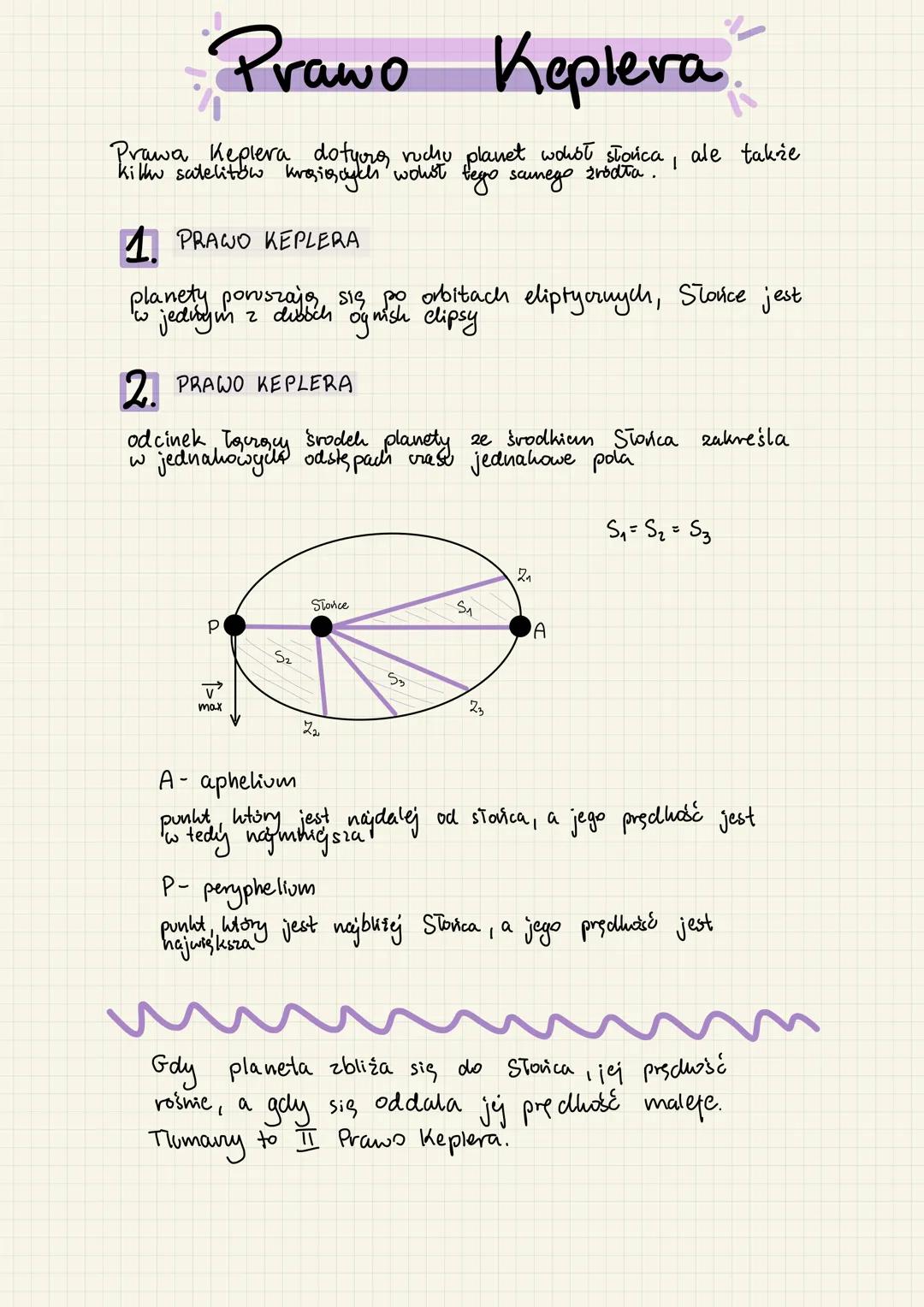
- Kepler's three laws describe planetary and satellite orbital motion patterns