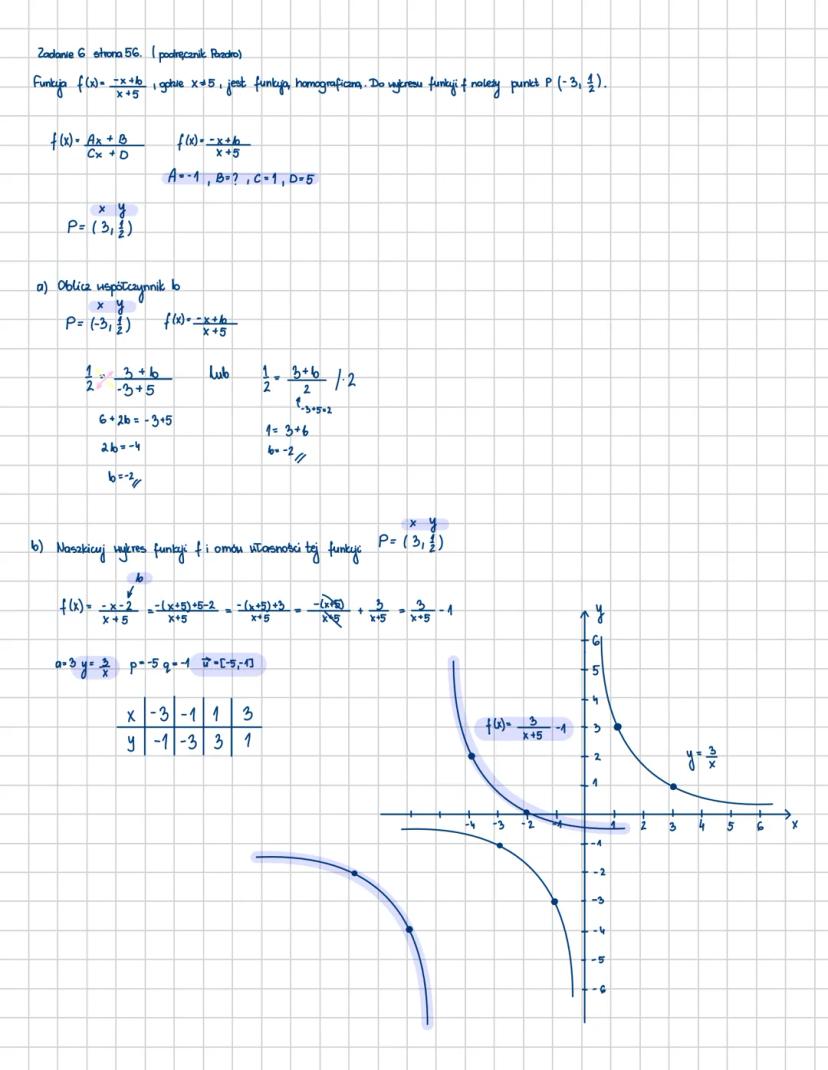
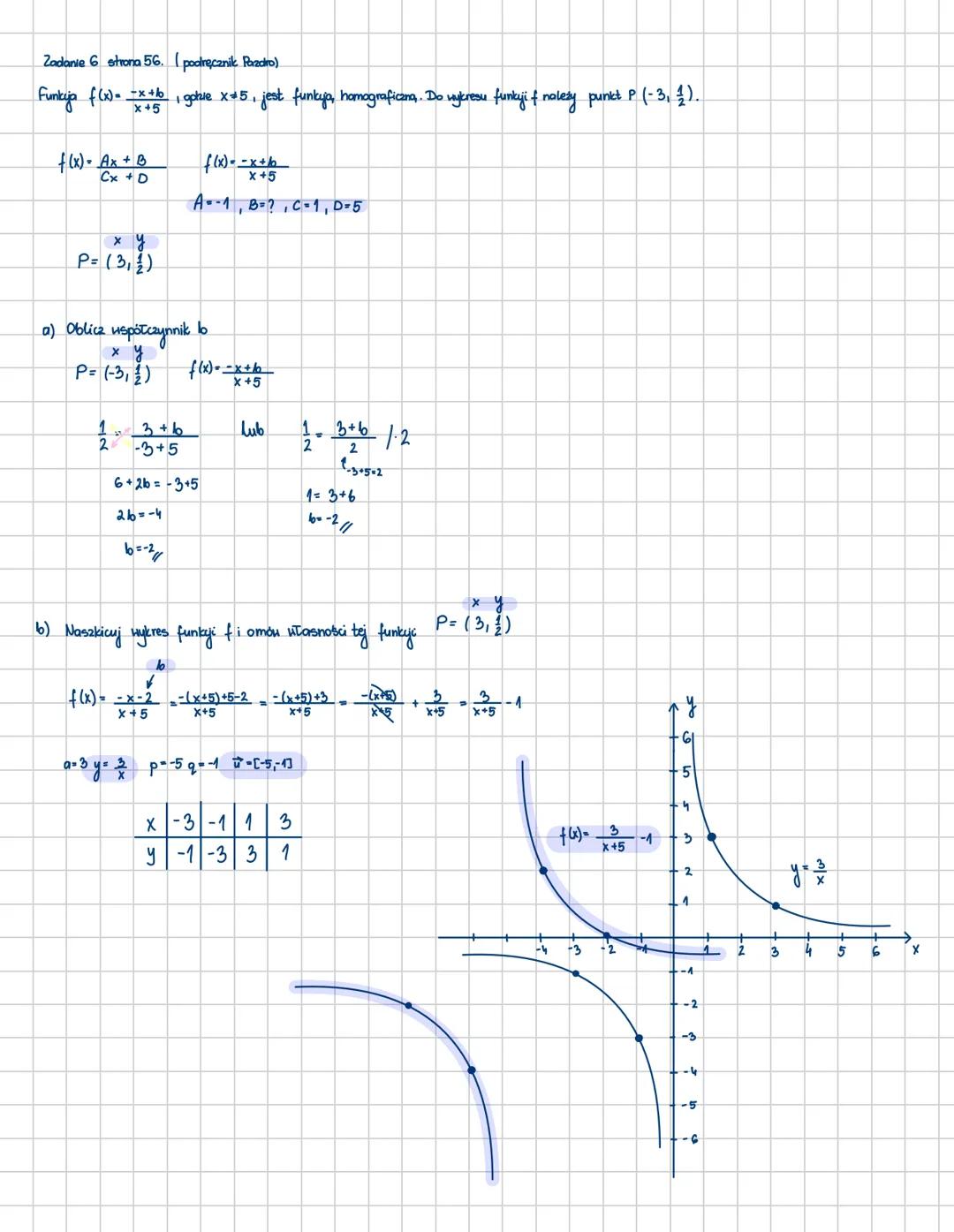
Charakterystyka funkcji homograficznej

Funkcja homograficzna ma postać y = $Ax + B$/$Cx + D$ i jej wykresem jest hiperbola. Przecina ona oś OX w punkcie $-D/C, 0$, a oś OY w punkcie $0, B/D$. Co ciekawe, funkcja ta nie ma miejsc zerowych, chyba że przesuniemy ją o wektor.

Warto zapamiętać, że funkcja homograficzna jest malejąca gdy a > 0, a rosnąca gdy a < 0. Nie posiada wartości największej ani najmniejszej, bo jej wykres rozciąga się w nieskończoność!

Po przesunięciu funkcji homograficznej o wektor [p, q], otrzymujemy funkcję postaci y = a/$x - p$ + q. Jej dziedzina to R{p}, a zbiór wartości to R{q}. Przy przekształceniach pamiętaj o zmianie znaku w wektorze, np. przy x - 3 - 7 wektor to [3, -7].

💡 Wskazówka: Przy rozwiązywaniu zadań najpierw sprowadź funkcję do postaci y = a/$x - p$ + q, a następnie odczytaj współczynniki i wektor przesunięcia!

Przykładowo, dla funkcji g(x) = $x + 4$/$x + 4$ możemy przekształcić ją do g(x) = $x + 4 - 4$/$x + 4$ + 1 = 1, gdzie a = -5, p = -1, q = 1, więc wektor przesunięcia to [-1, 1].

Zadania z przesunięciami funkcji homograficznych

Kiedy mamy funkcję i informację o jej przesunięciu o wektor, możemy znaleźć nową funkcję. Na przykład, funkcja y = 1/x przesunięta o wektor [-4, 3] daje funkcję h(x) = 1/$x + 4$ + 3.

Dziedzina i zbiór wartości nowej funkcji wynikają z przesunięcia. Dla powyższego przykładu dziedzina to R{-4}, a zbiór wartości to R{3}. Funkcja jest malejąca w przedziałach (-∞,-4) i (-4,∞).

Przy sprawdzaniu czy punkt należy do wykresu funkcji, podstaw jego współrzędne do wzoru i sprawdź czy równość jest spełniona. Na przykład, dla punktu A(-9, 2⅔) i funkcji h(x) = 1/$x + 4$ + 3, obliczamy: h(-9) = 1/(-9 + 4) + 3 = 1/(-5) + 3 = -1/5 + 3 = 2⅔.

🔍 Ważne: Aby znaleźć punkty wspólne wykresu funkcji homograficznej z inną funkcją (np. liniową), przyrównaj ich wzory i rozwiąż równanie, często kwadratowe!

Na przykład, aby znaleźć punkty wspólne h(x) = 1/$x + 4$ + 3 i y = x + 7, rozwiązujemy równanie 1/$x + 4$ + 3 = x + 7, co po przekształceniach daje x² + 8x + 15 = 0 i punkty (-5, 2) oraz (-3, 4).

Rozwiązywanie zadań z funkcją homograficzną

Kiedy masz funkcję f(x) = -x + b/$x - 5$ i wiesz, że przez jej wykres przechodzi punkt P(-3, 2), możesz obliczyć współczynnik b. Podstaw współrzędne punktu do wzoru funkcji:

f(-3) = -(-3) + b/(-3 - 5) = 3 + b/(-8) = 2

Po rozwiązaniu otrzymujesz: 3 - b/8 = 2, więc b = -8, a funkcja to f(x) = -x - 2/$x - 5$.

Funkcję homograficzną możemy przekształcić do postaci f(x) = -x - 2/$x - 5$ = -x + $x - 5 - x + 3$/$x - 5$ = -x + 1 - 2/$x - 5$. To pokazuje, że została ona przesunięta o wektor [5, -1].

🌟 Rada: Aby szybciej analizować funkcję homograficzną, sprowadź ją do postaci "bazowej" y = a/$x - p$ + q - od razu zobaczysz asymptoty i przesunięcie!

Możesz narysować wykres takiej funkcji zaznaczając asymptoty $x = 5 i y = -1$, kilka charakterystycznych punktów i szkicując dwie gałęzie hiperboli. Pamiętaj, że dla ujemnego współczynnika a funkcja jest rosnąca w swoich przedziałach dziedziny.