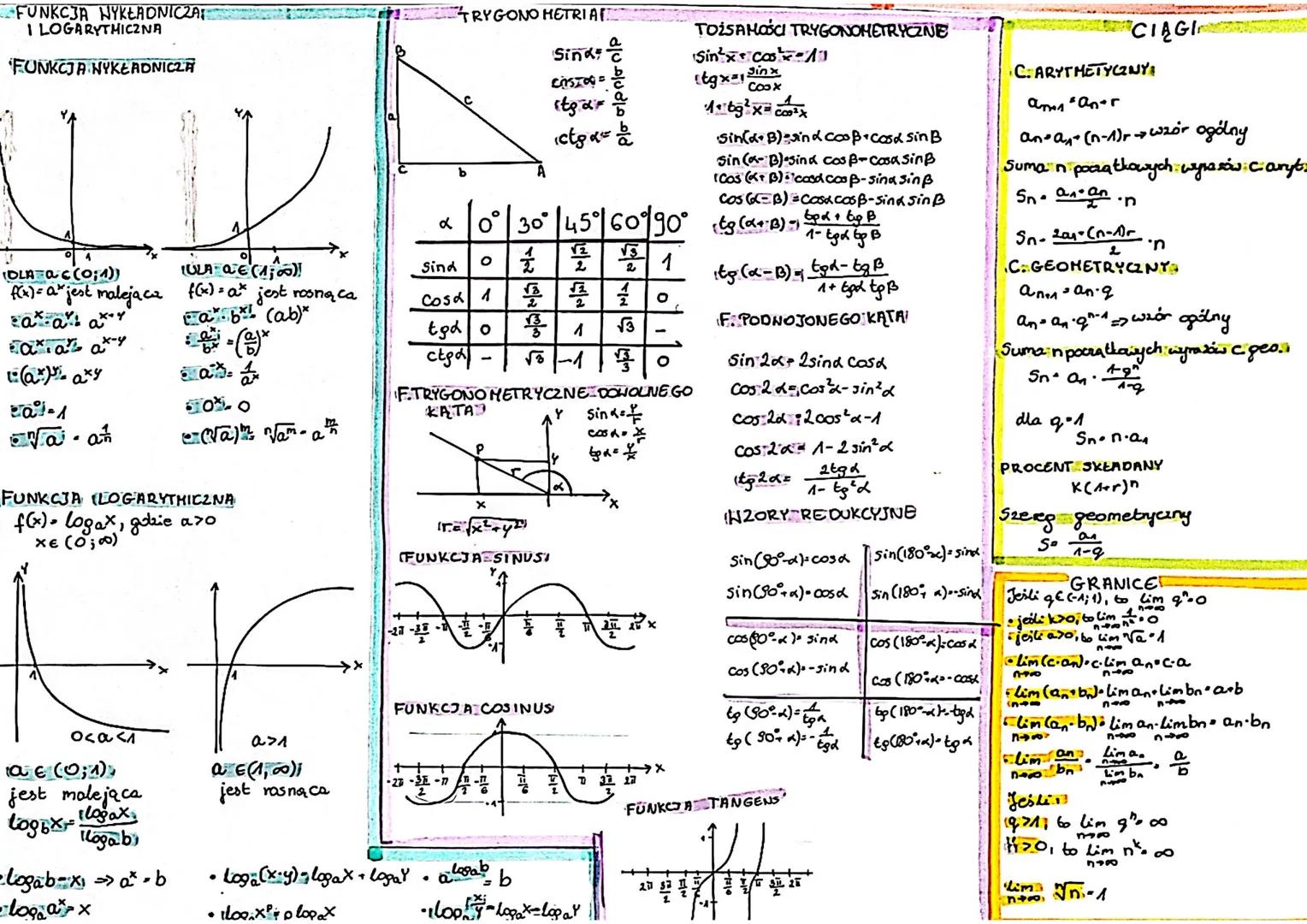
Funkcje wykładnicze i logarytmiczne - klucz do rozwiązywania równań

Funkcja wykładnicza f$x$ = aˣ zachowuje się różnie w zależności od podstawy a. Gdy a > 1, funkcja rośnie (im większe x, tym większa wartość), a gdy 0 < a < 1, funkcja maleje.

Pamiętaj o podstawowych wzorach na potęgi: aˣ · aʸ = aˣ⁺ʸ oraz aˣ/aʸ = aˣ⁻ʸ. Te wzory to podstawa rozwiązywania równań wykładniczych, więc warto je zapamiętać na pamięć.

Funkcja logarytmiczna f$x$ = log_a x to odwrotność funkcji wykładniczej. Najważniejsze wzory logarytmiczne to: log_a(xy) = log_a x + log_a y oraz log_a(x/y) = log_a x - log_a y. Dzięki nim możesz przekształcać skomplikowane wyrażenia logarytmiczne w prostsze.

Wskazówka: Logarytm to pytanie "do jakiej potęgi muszę podnieść podstawę a, żeby otrzymać x?" Jeśli to zrozumiesz, reszta pójdzie z górki!

Trygonometria - od trójkątów do funkcji

Funkcje trygonometryczne w trójkącie prostokątnym to sin α = a/c, cos α = b/c, tg α = a/b. Musisz znać na pamięć wartości dla kątów 30°, 45°, 60° - to podstawa każdego sprawdzianu z trygo.

Tożsamość podstawowa sin²x + cos²x = 1 to fundament całej trygonometrii. Z niej wyprowadzisz większość innych wzorów, więc jeśli ją zapamiętasz, reszta będzie łatwiejsza.

Wzory na sumę i różnicę kątów pozwalają ci rozłożyć sin$α + β$ czy cos$α - β$ na prostsze składniki. Szczególnie przydatne są wzory podwójnego kąta, jak sin 2α = 2sin α cos α.

Wzory redukcyjne pomagają przekształcić funkcje kątów większych niż 90° na funkcje kątów ostrych. Na przykład sin$90° - α$ = cos α.

Ciągi - matematyczne wzorce liczbowe

Ciąg arytmetyczny to taki, gdzie każdy następny wyraz otrzymujesz przez dodanie stałej liczby r (różnicy). Wzór ogólny to aₙ = a₁ + $n-1$r, a suma pierwszych n wyrazów: Sₙ = $a₁ + aₙ$/2 · n.

Ciąg geometryczny powstaje przez mnożenie poprzedniego wyrazu przez stałą liczbę q (iloraz). Tu wzór ogólny to aₙ = a₁ · qⁿ⁻¹, a suma: Sₙ = a₁$qⁿ-1$/$q-1$ dla q ≠ 1.

Procent składany K = K₀$1 + r$ⁿ to praktyczne zastosowanie ciągów geometrycznych w finansach. Jeśli |q| < 1, to suma szeregu geometrycznego wynosi S = a₁/$1-q$.

Pamiętaj: W ciągu arytmetycznym dodajesz, w geometrycznym mnożysz!

Granice - co się dzieje w nieskończoności

Granice ciągów mówią ci, do jakiej wartości zmierza ciąg, gdy n dąży do nieskończoności. Jeśli |q| < 1, to qⁿ zmierza do 0, a jeśli q > 1, to qⁿ rośnie do nieskończoności.

Działania na granicach są intuicyjne: granica sumy to suma granic, granica iloczynu to iloczyn granic. Przy dzieleniu musisz tylko sprawdzić, czy mianownik nie zmierza do zera.

Szczególnie ważna jest granica ⁿ√A = 1 dla dowolnego A > 0. Ten wzór często ratuje sytuację w trudnych zadaniach z granicami.