Podstawowe figury geometryczne

Geometria płaska opiera się na kilku kluczowych figurach, które warto dobrze poznać. Kwadrat ma wszystkie boki równe i wszystkie kąty proste - jego pole to a², a obwód to 4a. Prostokąt ma równe boki naprzeciwległe i wszystkie kąty proste - pole wynosi a·b, a obwód 2a+2b.

Trójkąt to podstawowa figura geometryczna o trzech bokach. Jego pole możesz obliczyć jako połowę iloczynu podstawy i wysokości $P=½·a·h$. Dla trójkąta znasz też twierdzenie Pitagorasa $a²+b²=c²$, które stosuje się w trójkątach prostokątnych.

Równoległobok ma przeciwległe boki równoległe i równej długości. Jego pole obliczysz mnożąc długość boku przez wysokość $P=a·h$. Trapez ma tylko jedną parę boków równoległych, a jego pole to P=½$a+b$·h.

Ciekawostka! Czy wiesz, że każdy trójkąt ma dokładnie trzy środkowe, trzy wysokości i trzy dwusieczne kątów? Te linie przecinają się odpowiednio w środku ciężkości, ortocentrum i środku okręgu wpisanego.

Własności figur płaskich

Każda figura płaska ma swoje charakterystyczne cechy i wzory. Kwadrat ma przekątną o długości a√2, a jego pole to a². Prostokąt ma przekątną równą √$a²+b²$, która dzieli go na dwa przystające trójkąty.

Trójkąt to najbardziej wszechstronna figura geometryczna. Pole trójkąta możesz obliczyć na kilka sposobów: P=½·a·h (z wysokością), P=½·a·b·sinα (z dwoma bokami i kątem) lub P=√$p(p-a)(p-b)(p-c)$ (wzór Herona, gdzie p to połowa obwodu).

Trapez ma dwa boki równoległe (a i b) oraz wysokość h, co pozwala obliczyć jego pole jako P=½$a+b$·h. Romb to czworokąt o wszystkich bokach równych - jego pole możesz obliczyć jako P=½·e·f (gdzie e i f to długości przekątnych).

Bardzo ważną koncepcją w geometrii jest podobieństwo trójkątów. Dwa trójkąty są podobne, gdy mają odpowiadające kąty równe i odpowiadające boki proporcjonalne. Skala podobieństwa k wpływa na stosunek obwodów $k$, pól (k²) i objętości brył (k³).

Wskazówka! Zapamiętaj, że w podobnych figurach stosunek pól jest kwadratem skali podobieństwa, a to pomoże ci rozwiązać wiele zadań!

Wielokąty i koło

Trójkąty charakterystyczne warto zapamiętać: trójkąt 30°-60°-90° (o bokach a, a√3, 2a) oraz trójkąt 45°-45°-90° (o bokach a, a, a√2). Trójkąt równoboczny ma wszystkie boki i kąty równe - jego wysokość to a√3/2.

Koło to zbiór wszystkich punktów oddalonych od środka o odległość nie większą niż promień R. Jego pole wynosi πR², a długość okręgu 2πR. Dla wycinka koła pole obliczysz jako $α/360°$·πR², gdzie α to miara kąta środkowego w stopniach.

Sześciokąt foremny to wielokąt o sześciu równych bokach i kątach. Jego pole możesz obliczyć jako 6·$a²√3/4$, gdzie a to długość boku. Promień okręgu opisanego na takim sześciokącie wynosi R=a.

Twierdzenie Talesa mówi, że jeśli dwie proste są przecięte prostymi równoległymi, to odcinki powstałe na pierwszej prostej są proporcjonalne do odpowiadających im odcinków na drugiej prostej.

Zapamiętaj! W praktyce warto znać podstawowe jednostki miary: 1 hektar (ha) = 10000 m², 1 ar $a$ = 100 m². Łatwo popełnić błąd przy przeliczaniu, więc zawsze sprawdzaj jednostki!

Pojęcia podstawowe geometrii płaskiej

Geometria płaska zaczyna się od podstawowych pojęć. Punkt nie ma wymiarów, a prosta jest nieograniczoną linią prostą. Półprosta to część prostej ograniczona z jednej strony punktem. Odcinek to fragment prostej ograniczony dwoma punktami.

Kąty klasyfikujemy według ich miary: zerowy $α=0°$, ostry (0°<α<90°), prosty $α=90°$, rozwarty (90°<α<180°), półpełny $α=180°$, wklęsły (180°<α<360°) i pełny $α=360°$. Wyróżniamy też kąty wierzchołkowe (równe sobie), przyległe (suma 180°), naprzemianległe i odpowiadające.

Figura wypukła to taka, w której każdy odcinek łączący dwa punkty należące do figury, w całości zawiera się w tej figurze. Innymi słowy, figura wypukła nie ma żadnego "wklęśnięcia" i wszystkie jej kąty wewnętrzne są mniejsze od 180°. Przykładami są koło, trójkąt czy kwadrat.

Figura ograniczona to taka, którą można w całości zmieścić wewnątrz pewnego koła. Odcinek, trójkąt, koło są figurami ograniczonymi, podczas gdy prosta czy półprosta są nieograniczone.

Podpowiedź! Aby łatwo rozpoznać figurę wypukłą, sprawdź czy da się połączyć dowolne dwa punkty tej figury odcinkiem, który w całości należy do figury!

Obliczanie miar kątów

Zadania z kątami to podstawa geometrii płaskiej. W zadaniu pierwszym mamy dwa przykłady do rozwiązania. W przykładzie a) musimy odnaleźć kąt α znając kąt 130°. Ponieważ widzimy układ kątów przyległych, możemy napisać: α + 130° = 180° (suma kątów przyległych). Stąd α = 50°.

W przykładzie b) występują kąty utworzone przez dwie proste przecięte trzecią prostą. Znając kąt 110°, możemy wykorzystać własności kątów naprzemianległych oraz fakt, że suma kątów w trójkącie wynosi 180°.

Zwróć uwagę na relacje między kątami - gdy dwie proste są przecięte trzecią, powstają kąty odpowiadające (równe sobie) oraz naprzemianległe (też równe). Te zależności pozwalają rozwiązać większość zadań z kątami.

Wskazówka! Zawsze szukaj kątów przyległych (suma 180°), wierzchołkowych (są równe) lub naprzemianległych (też równe). Pomoże ci to znaleźć brakujące miary kątów!

Figury wklęsłe i wypukłe

Rozpoznawanie figur wklęsłych i wypukłych to ważna umiejętność w geometrii. Figury wypukłe to takie, w których każdy odcinek łączący dowolne dwa punkty figury leży w całości wewnątrz tej figury. Figury wklęsłe mają przynajmniej jedno "wklęśnięcie" - czyli istnieją w nich takie punkty, że odcinek je łączący wychodzi częściowo poza figurę.

W zadaniu 2 trzeba zaklasyfikować różne figury. Figura A to typowa figura wklęsła - ma wyraźne wcięcie. Figura B jest prawdopodobnie wypukła, ponieważ każdy odcinek łączący dwa jej punkty leży w całości wewnątrz niej.

Analizując pozostałe figury, zwróć uwagę na ich kształt - jeśli figura ma jakiekolwiek "wcięcie", to jest wklęsła. Jeśli nie ma żadnych wcięć, to jest wypukła. Niektóre figury mogą być ani wklęsłe, ani wypukłe - na przykład jeśli składają się z rozłącznych części.

Sprawdź! Aby szybko rozpoznać figurę wklęsłą, narysuj odcinek łączący dwa punkty figury. Jeśli choć jeden taki odcinek wychodzi poza figurę - jest ona wklęsła!

Wzajemne położenie prostych i odległości

W geometrii analitycznej bardzo przydatne są wzory na odległość punktu od prostej. Jeśli masz punkt P=(x₀,y₀) i prostą k: Ax+By+C=0, to odległość między nimi wynosi:

d = |Ax₀+By₀+C|/√$A²+B²$

Prostą y=2x-5 należy najpierw przekształcić do postaci ogólnej, czyli -2x+y+5=0 $stąd A=-2, B=1, C=5$. Podstawiając punkt A=(3,4) do wzoru, otrzymujemy:

d = |$-2$·3+1·4+5|/√$(-2)²+1²$ = |3|/√5 = 3√5/5

Dla prostych równoległych k: Ax+By+C=0 i m: Ax+By+D=0 odległość wynosi: d = |C-D|/√$A²+B²$

Symetralna odcinka to prosta prostopadła do tego odcinka, przechodząca przez jego środek. Aby ją wyznaczyć, należy znaleźć środek odcinka i kierunek prostopadły do prostej przechodzącej przez końce odcinka.

Ważne! Gdy obliczasz odległość punktu od prostej, pamiętaj o sprowadzeniu równania prostej do postaci ogólnej Ax+By+C=0. Następnie podstaw współrzędne punktu do wzoru!

Odległości w geometrii analitycznej

Obliczanie odległości to kluczowa umiejętność w geometrii analitycznej. Aby obliczyć odległość punktu B=(0,3) od prostej l: 3x-y-7=0, stosujemy wzór d = |Ax₀+By₀+C|/√$A²+B²$, gdzie A=3, B=-1, C=-7, a punkt ma współrzędne x₀=0, y₀=3:

d = |3·0+$-1$·3+$-7$|/√$3²+(-1)²$ = |$-3$+$-7$|/√10 = 10/√10 = √10

Dla punktu C=$-1,3$ i prostej m: x-3y=-3, najpierw sprowadzamy równanie do postaci ogólnej: x-3y+3=0. Następnie podstawiamy do wzoru, gdzie A=1, B=-3, C=3, x₀=-1, y₀=3:

d = |1·$-1$+$-3$·3+3|/√$1²+(-3)²$ = |$-1$+$-9$+3|/√10 = |-7|/√10 = 7/√10 = 7√10/10

Przy obliczaniu odległości między prostymi równoległymi, używamy wzoru d = |C-D|/√$A²+B²$. Dla prostych k: x+2y-1=0 i l: x+2y-6=0 mamy:

d = |$-1$-$-6$|/√$1²+2²$ = |5|/√5 = √5

Pamiętaj! Gdy masz prostą w postaci kierunkowej y=ax+b, przekształć ją do postaci ogólnej Ax+By+C=0, by móc skorzystać z gotowych wzorów na odległości.

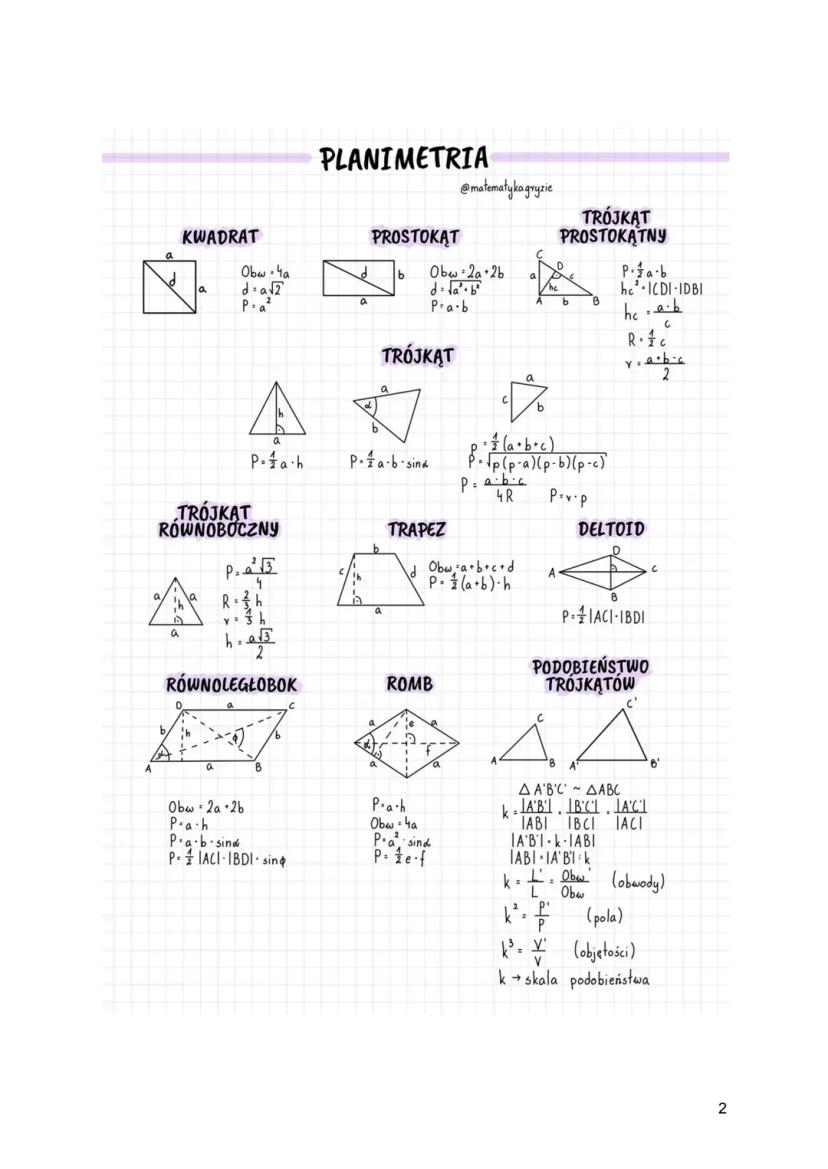
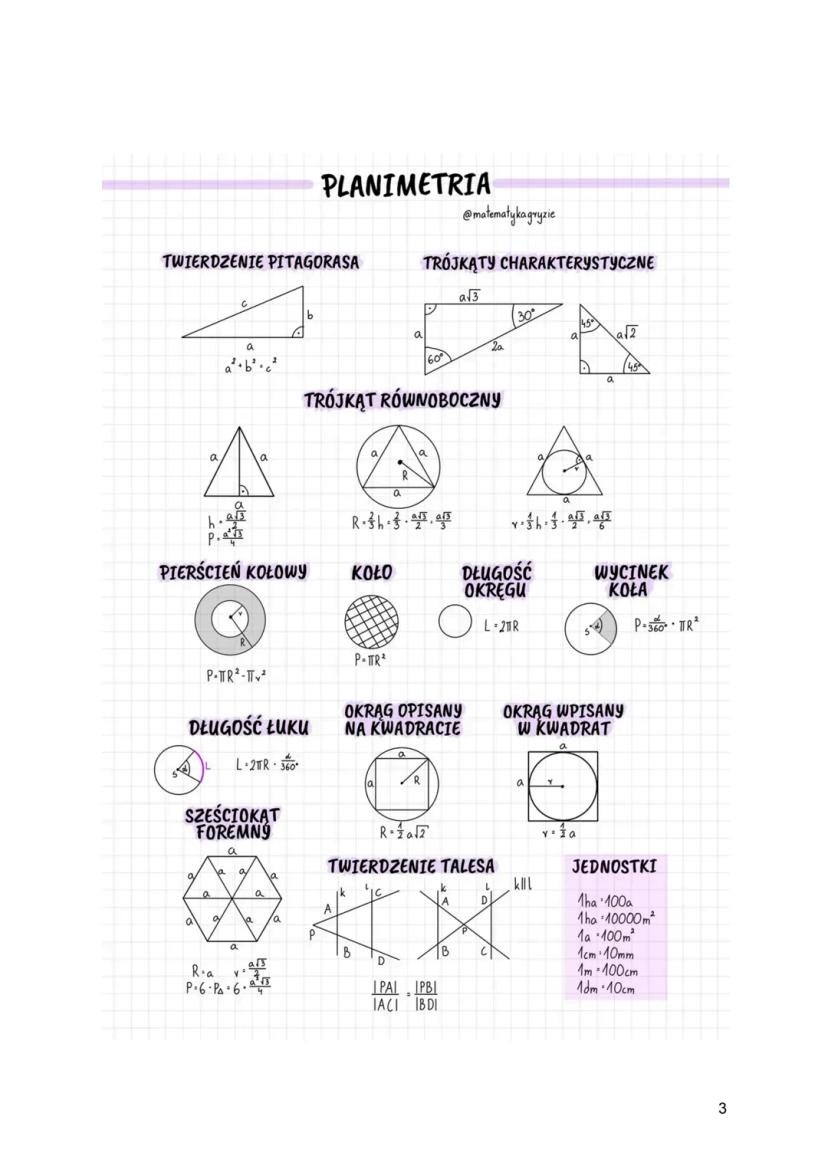
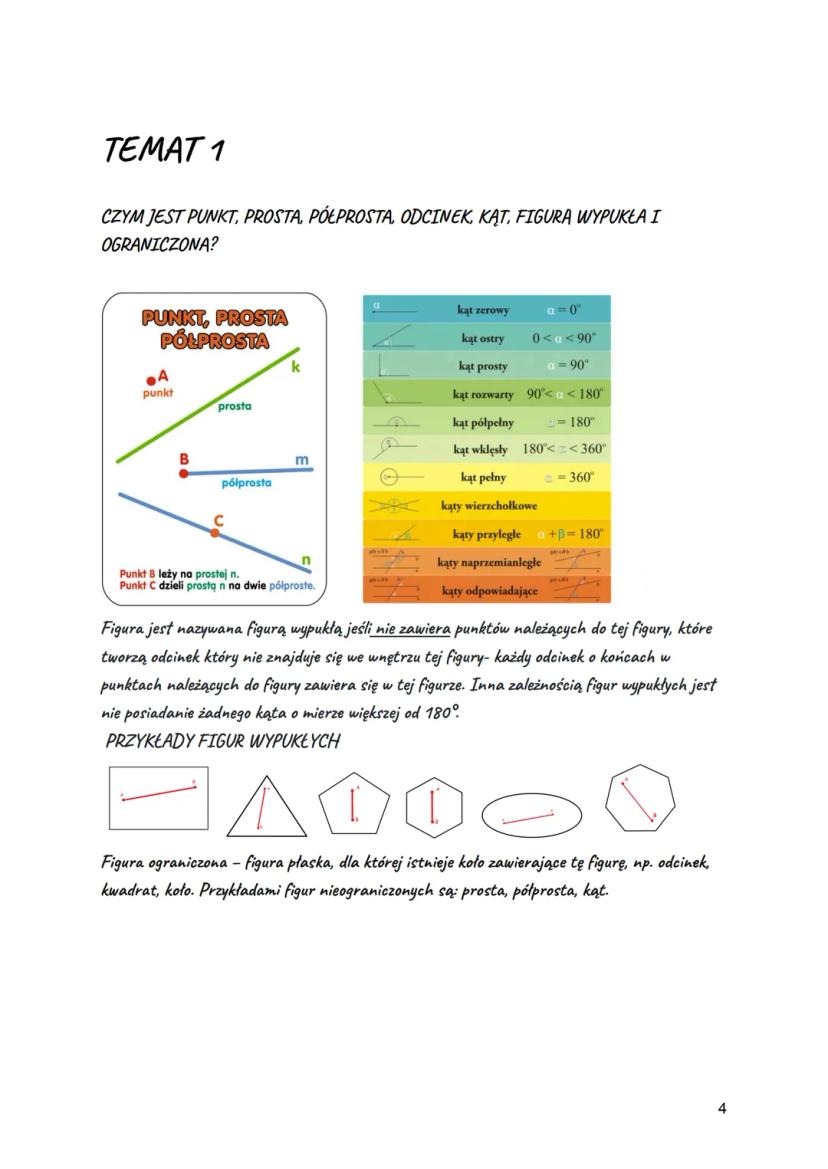
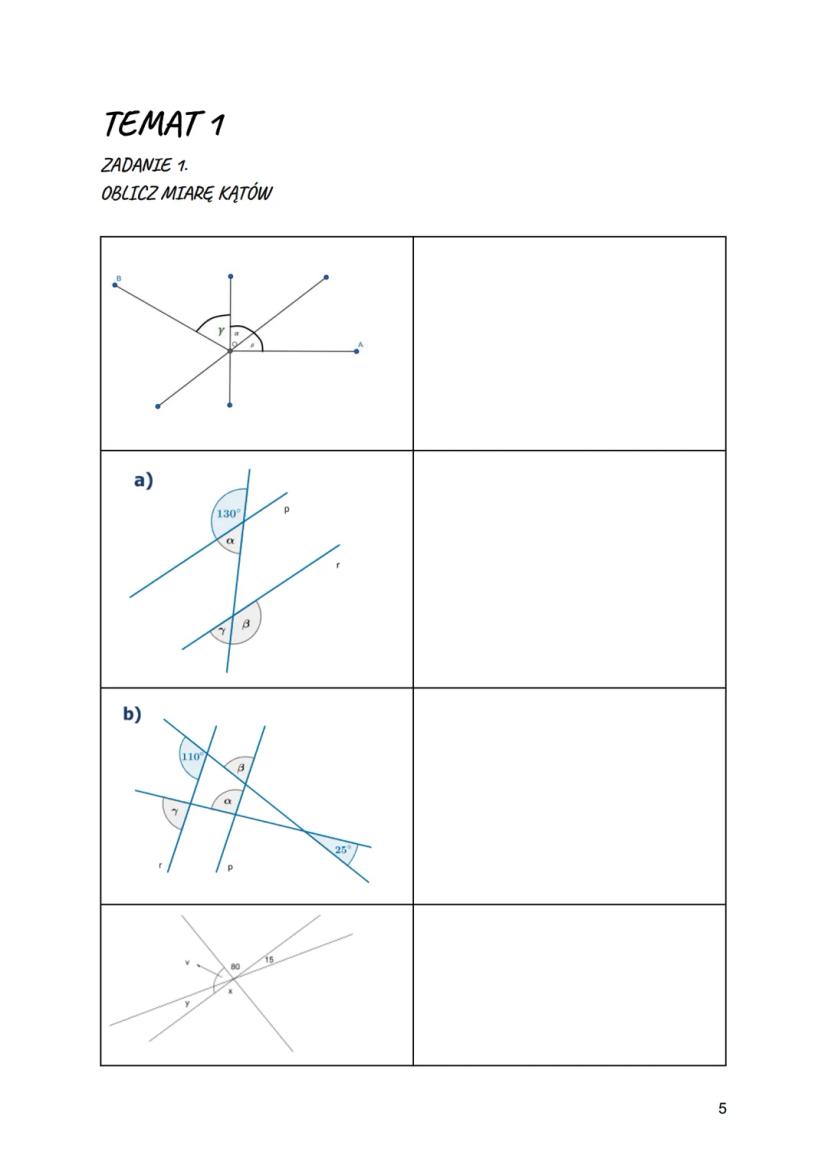
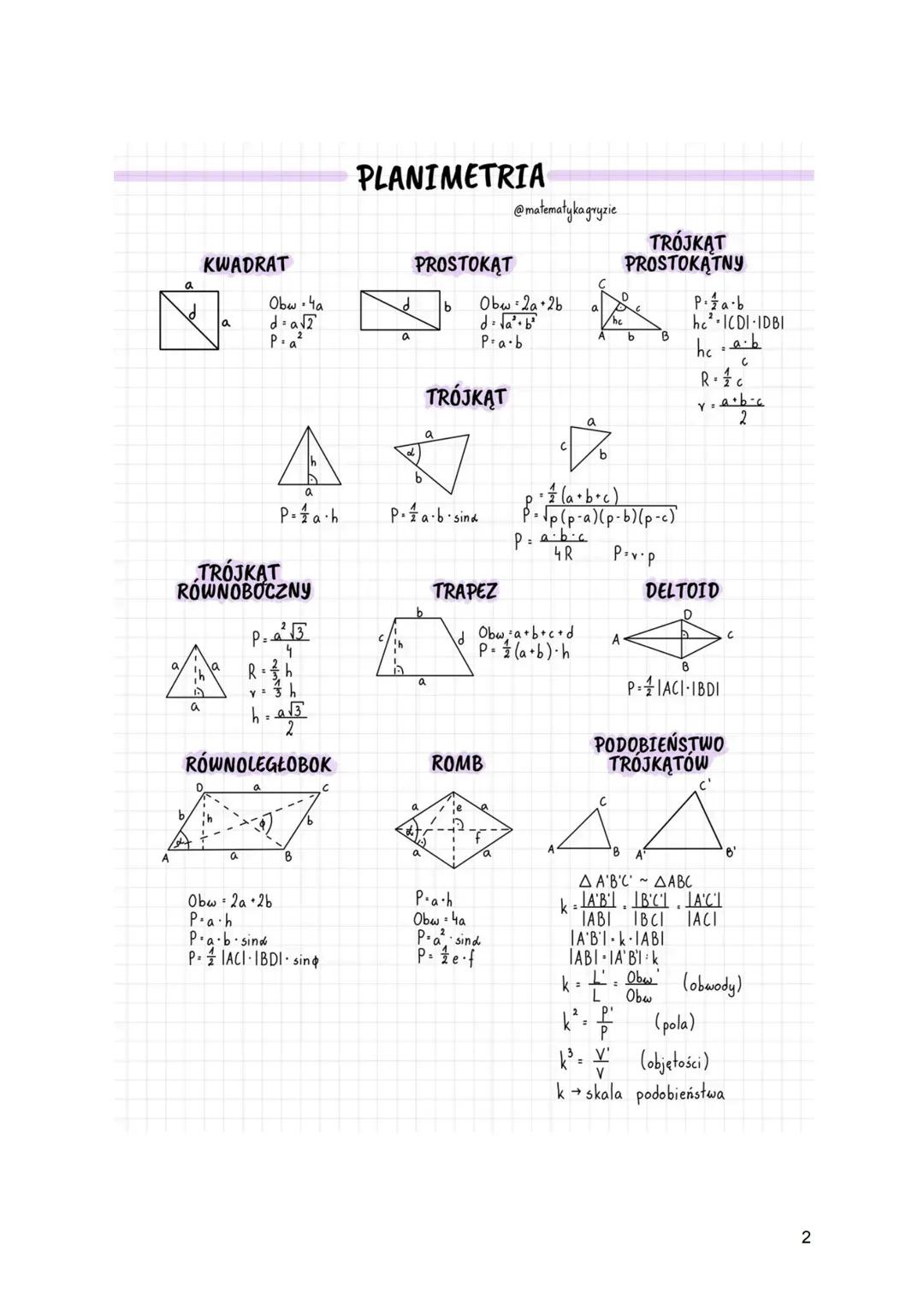
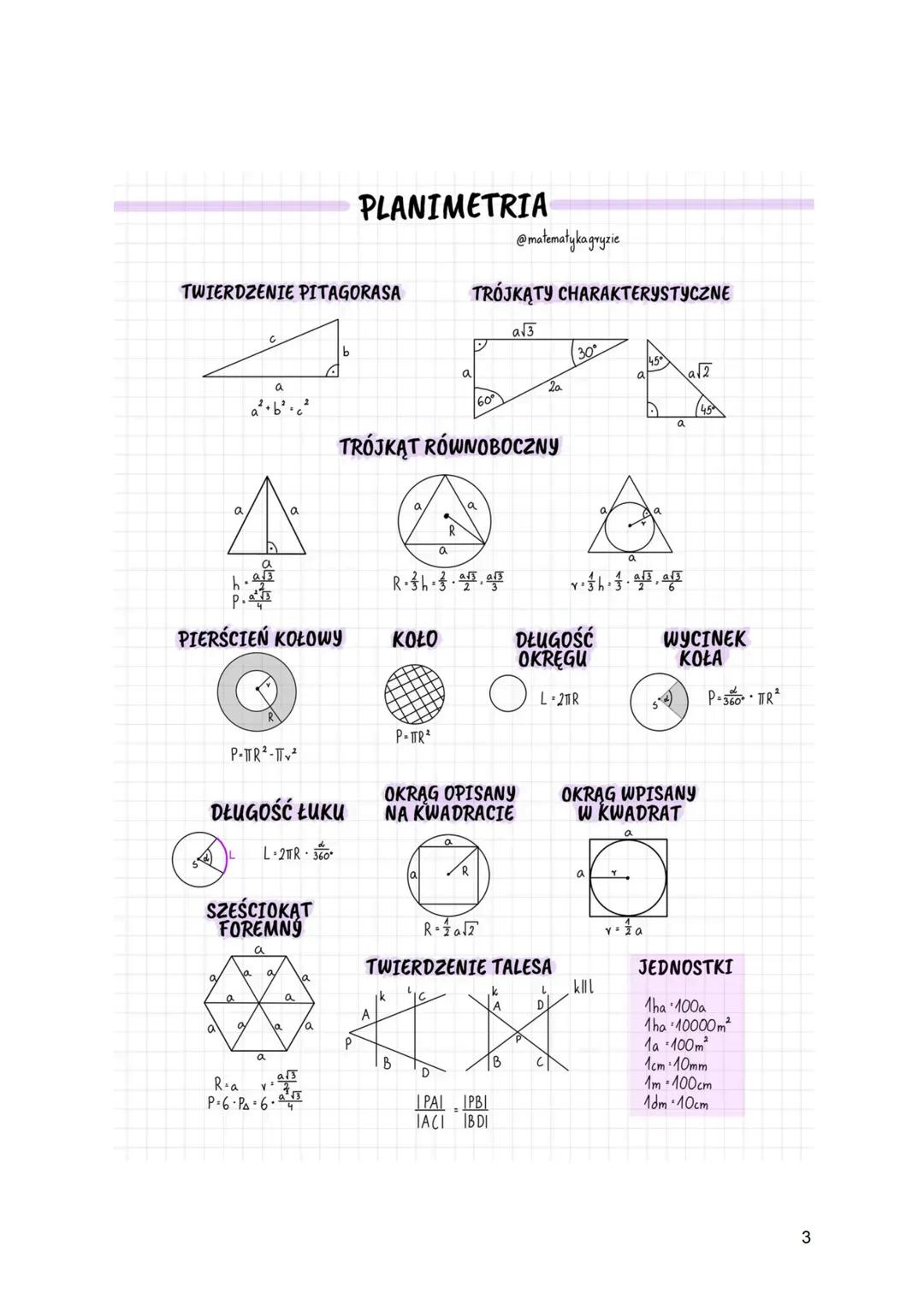
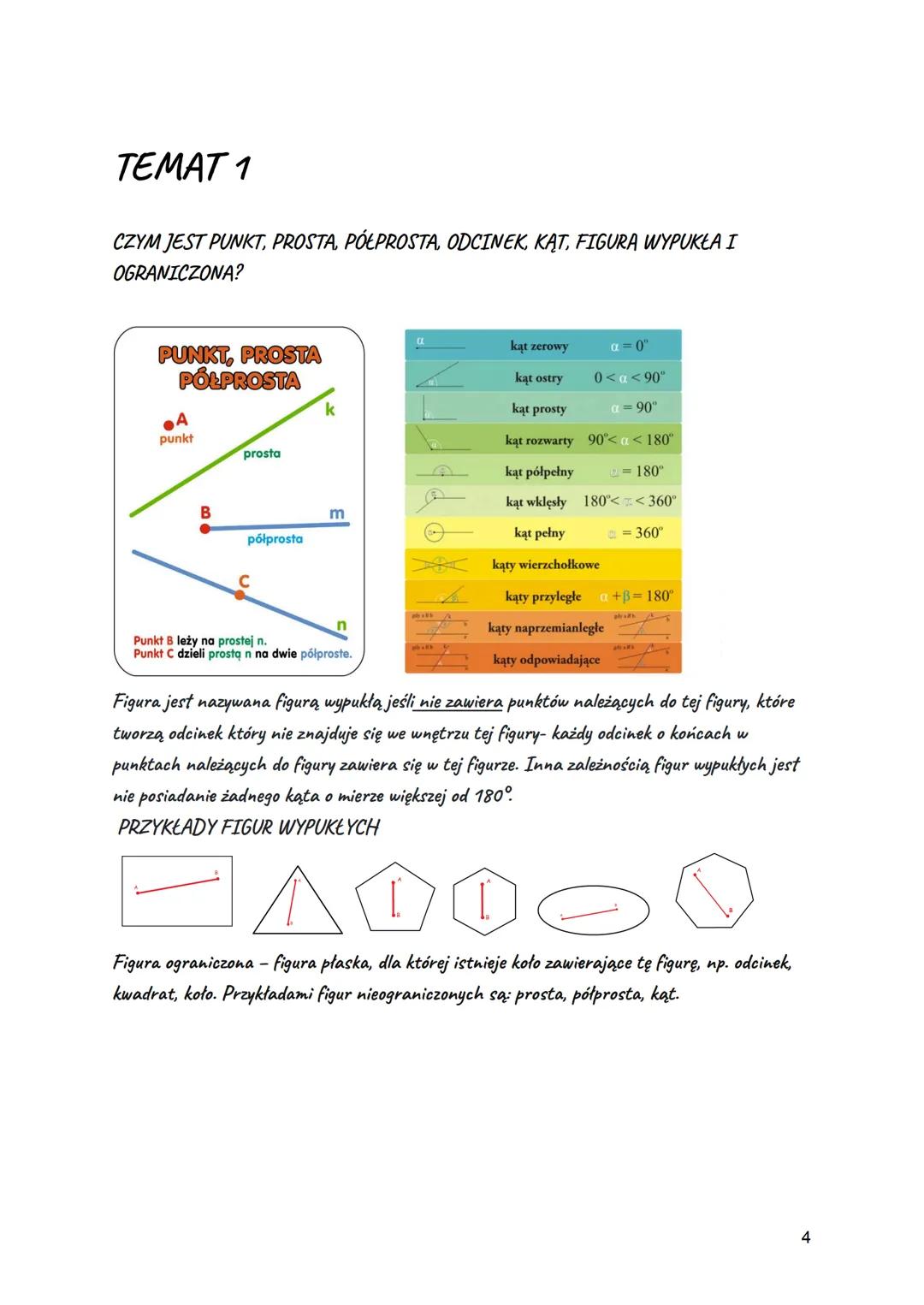
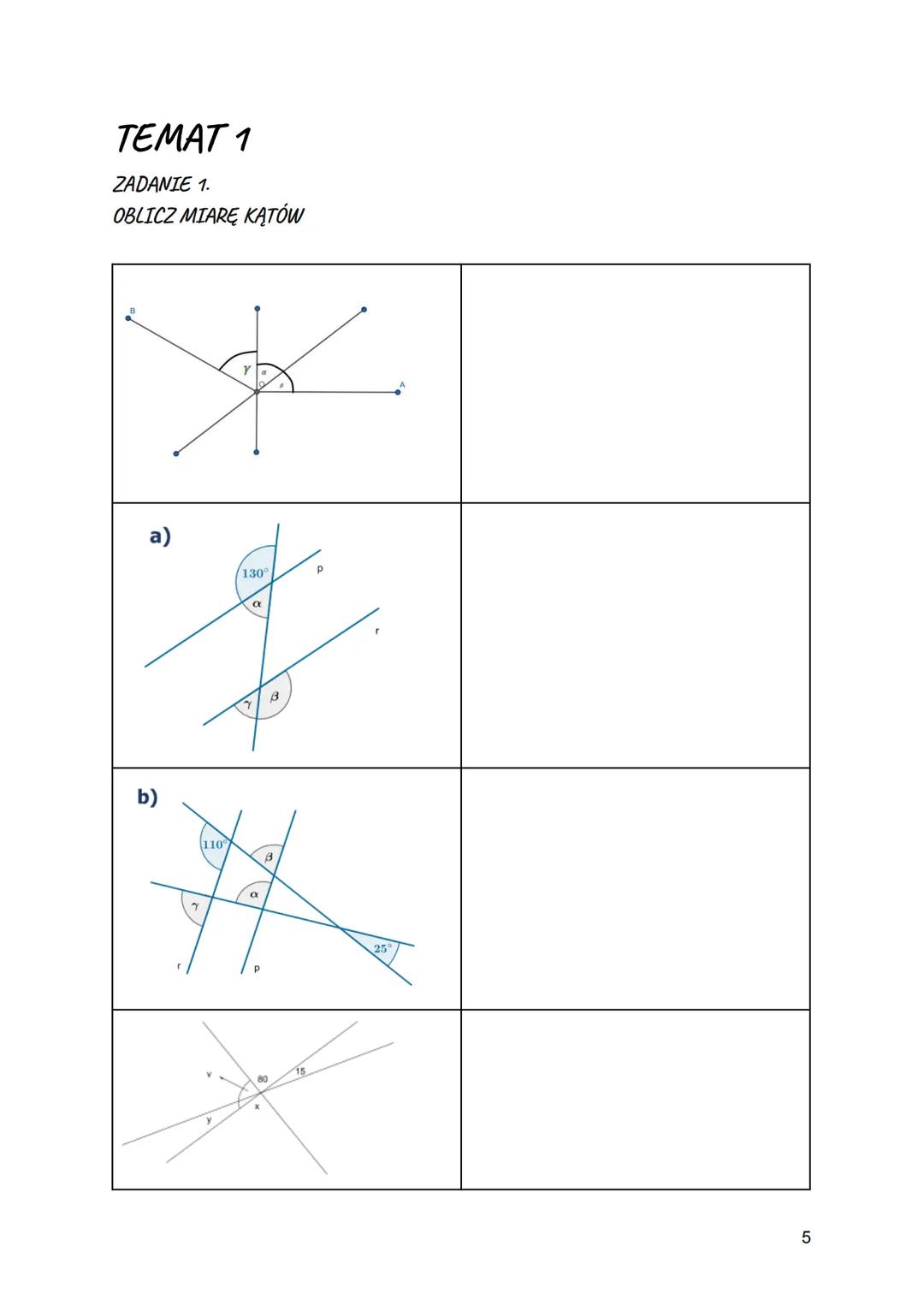
Symetralna odcinka

Symetralna odcinka to prosta prostopadła do niego, przechodząca przez jego środek. Jej wyznaczanie to ważna umiejętność geometryczna. Aby wyznaczyć symetralną odcinka AB, gdzie A=$-2,2$ i B=(2,10), wykonujemy trzy kroki:

Najpierw wyznaczamy równanie prostej AB. Tworzymy układ równań podstawiając współrzędne punktów: 2 = -2a + b 10 = 2a + b

Rozwiązując układ, otrzymujemy a=2 i b=6, więc prosta ma równanie y=2x+6.

Następnie obliczamy środek odcinka AB ze wzoru S=$(x₁+x₂)/2, (y₁+y₂)/2$: S = $(-2+2)/2, (2+10)/2$ = (0,6)

Na końcu wyznaczamy równanie symetralnej. Ponieważ symetralna jest prostopadła do prostej AB, a iloczyn współczynników kierunkowych prostych prostopadłych wynosi -1, to: a₁ · a₂ = -1, stąd a₂ = -1/2 $bo a₁=2$

Równanie symetralnej ma więc postać y = -1/2x + b. Podstawiając współrzędne punktu S(0,6), otrzymujemy: 6 = -1/2 · 0 + b, więc b=6

Ostateczne równanie symetralnej to y = -1/2x + 6.

Wskazówka! Symetralna jest miejscem geometrycznym punktów równo oddalonych od końców odcinka - ta własność jest często wykorzystywana w konstrukcjach geometrycznych.

Ćwiczenia z symetralnej odcinka

Mając punkty A=$-1,1$ i B=$5,-1$, wyznaczmy równanie symetralnej odcinka AB. Postępujemy podobnie jak w poprzednim przykładzie:

Krok 1: Wyznaczamy równanie prostej AB. Tworzymy układ równań: 1 = -1a + b -1 = 5a + b

Po odjęciu stronami: 2 = -6a a = -1/3 b = 2/3

Prosta AB ma równanie y = -1/3x + 2/3.

Krok 2: Obliczamy środek odcinka AB: S = $(-1+5)/2, (1+(-1))/2$ = (2,0)

Krok 3: Wyznaczamy równanie symetralnej. Ponieważ prosta AB ma współczynnik kierunkowy a = -1/3, to symetralna ma współczynnik a = 3 $bo -1/3 · 3 = -1$.

Równanie symetralnej ma postać y = 3x + b. Punkt S(2,0) leży na symetralnej, więc: 0 = 3 · 2 + b 0 = 6 + b b = -6

Ostateczne równanie symetralnej to y = 3x - 6.

Sprawdź swoje rozwiązanie! Każdy punkt leżący na symetralnej powinien być jednakowo oddalony od punktów A i B. Możesz to potwierdzić, wybierając dowolny punkt na symetralnej i obliczając jego odległości od A i B.