Wartość bezwzględna i równania

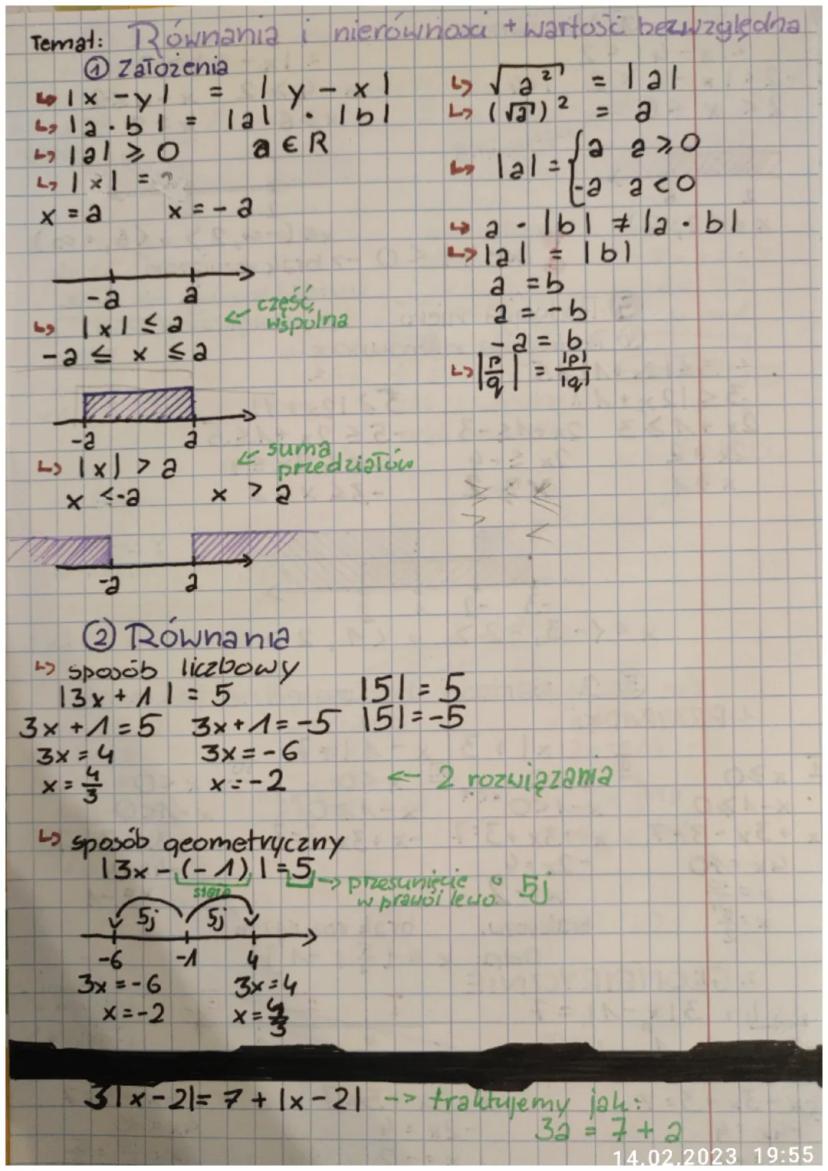
Wartość bezwzględna liczby, oznaczana jako |a|, to odległość liczby od zera na osi liczbowej. Pamiętaj, że:

• Jeśli a ≥ 0, to |a| = a
• Jeśli a < 0, to |a| = -a

Równania z wartością bezwzględną możemy rozwiązywać na dwa sposoby: liczbowo i geometrycznie. W metodzie liczbowej rozbijamy równanie na przypadki. Na przykład, dla |3x+1|=5:

• Jeśli 3x+1 ≥ 0, to 3x+1 = 5, więc x = 4/3
• Jeśli 3x+1 < 0, to -$3x+1$ = 5, więc x = -2

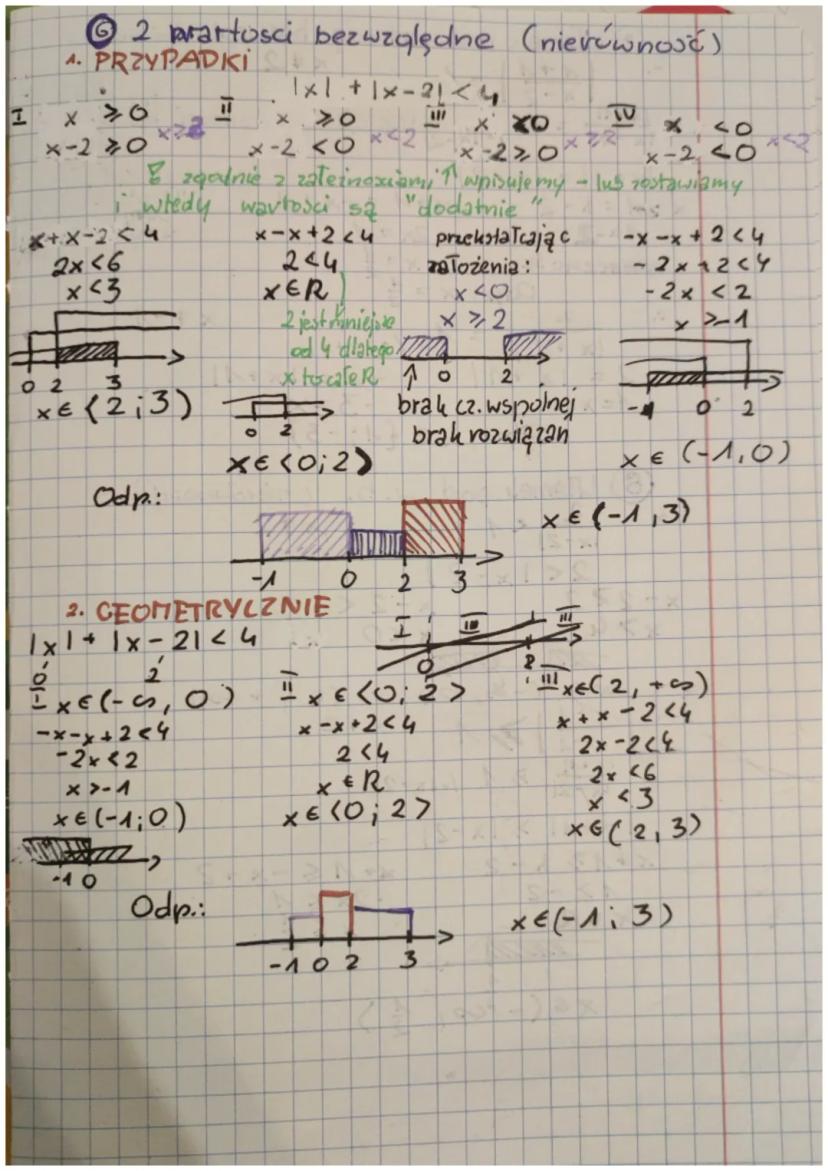
💡 Wskazówka: W metodzie geometrycznej myślimy o wartości bezwzględnej jako odległości. Na przykład |x-4|=2 oznacza, że szukamy punktów oddalonych o 2 od punktu 4 na osi liczbowej.

Przy rozwiązywaniu równań typu |x-a|=b, gdzie b > 0, otrzymujemy dwa rozwiązania: x = a+b lub x = a-b. Jeżeli równanie ma postać |x-a|=0, to jedynym rozwiązaniem jest x = a.

Nie bój się tych zadań! Rozwiązując równania z wartością bezwzględną, zawsze zastanów się nad znakiem wyrażenia wewnątrz.

Nierówności z wartością bezwzględną

Nierówności z wartością bezwzględną to zadania, w których zamiast znaku równości pojawia się znak nierówności. Dla przykładu |x-4|<2 oznacza:

• -2 < x-4 < 2
• Co daje: 2 < x < 6

Zapamiętaj, że nierówność |x-a|<b przedstawia przedział $a-b; a+b$, czyli punkty oddalone od a o mniej niż b. Natomiast nierówność |x-a|≥b to punkty oddalone od a o co najmniej b, czyli przedział $-∞; a-b]∪[a+b; +∞$.

Przy podwójnych nierównościach, jak 3≤|2x+1|≤5, rozwiązujemy dwie nierówności:

1. |2x+1|≥3, czyli 2x+1≥3 lub 2x+1≤-3
2. |2x+1|≤5, czyli -5≤2x+1≤5

💡 Pamiętaj: Wartość bezwzględna nigdy nie jest ujemna! Dlatego nierówność typu |x|<0 nie ma rozwiązań.

Rozwiązanie znajdujemy jako część wspólną obu zbiorów. W tym przykładzie x∈⟨-3,-2⟩∪⟨1,2⟩. Rysowanie osi liczbowej pomoże Ci lepiej zrozumieć te zakresy.

Nierówności z dwoma wartościami bezwzględnymi

Równania i nierówności z dwiema wartościami bezwzględnymi możemy rozwiązywać dzieląc rozwiązanie na przypadki lub geometrycznie. Rozważmy przykład |x|+3|x-1|=7:

Metoda przypadków polega na analizowaniu różnych przedziałów, w których wyrażenia pod wartościami bezwzględnymi mają stały znak:

1. Gdy x ≥ 0 i x ≥ 1: x+3$x-1$=7, więc x = 5/2
2. Gdy x ≥ 0 i x < 1: x+3$1-x$=7, więc x = -1
3. Gdy x < 0 i x < 1: -x+3$1-x$=7, stąd x = -2

Przy nierównościach, jak |x|+|x-2|<4, również rozbijamy na przypadki:

1. Gdy x < 0: -x-x+2 < 4, więc x > -1
2. Gdy 0 ≤ x < 2: x+2-x < 4, co jest zawsze prawdą
3. Gdy x ≥ 2: x+x-2 < 4, więc x < 3

💡 Metoda geometryczna: Możesz myśleć o |x|+|x-2| jako o sumie odległości punktu x od 0 i od 2 na osi liczbowej.

Łącząc wszystkie przedziały otrzymujemy rozwiązanie: x∈⟨-1;3⟩. Sprawdź zawsze, czy żaden przedział nie został pominięty!

Ułamki z wartością bezwzględną

Równania z ułamkami zawierającymi wartości bezwzględne wymagają szczególnej uwagi. Najpierw musimy określić dziedzinę wyrażenia - na przykład, w równaniu |x+1|/|x-2| = 1, musimy pamiętać, że x ≠ 2.

Rozwiązując równanie |x+1|/|x-2| = 1:

1. Upraszczamy do |x+1| = |x-2|
2. Rozważamy przypadki:
   • Gdy x+1 = x-2, otrzymujemy sprzeczność
   • Gdy x+1 = -$x-2$, czyli x+1 = -x+2, stąd x = 1/2

Dla nierówności typu 2/|x-2| < 1:

1. Pamiętamy, że x ≠ 2
2. Przekształcamy do 2 < |x-2|
3. Rozbijamy na: x-2 > 2 (czyli x > 4) lub x-2 < -2 (czyli x < 0)

💡 Ważne: Przy ułamkach zawsze sprawdź dziedzinę! Wartość w mianowniku nie może być zerem.

Nierówności typu |x+1|/|x-2| > 1 rozwiązujemy podobnie, przekształcając je do |x+1| > |x-2|, a następnie analizując przypadki zależne od znaków wyrażeń pod wartościami bezwzględnymi. W tym przykładzie otrzymujemy x ∈ $-∞, 1/2$.