Zacznij

Matematyka

Twierdzenia o przystawaniu i podobieństwie trójkątów

twierdzenia geometryczne

Matematyka2346Zaktualizowano 11 wrz 20267 strony

Trójkąty - Rodzaje i Właściwości

Zgłoś
user profile picture
Patrix Patryk@patrix_son.1369
Dodaj do źródeł Google
Trójkąty to jeden z najważniejszych tematów w geometrii, który będzie Ci towarzyszył przez całą szkołę średnią. Poznasz wszystkie rodzaje trójkątów, sposoby obliczania ich pól oraz kluczowe twierdzenia, które pomogą Ci rozwiązywać nawet skomplikowane zadania.
Trójkąty – strona 1

Zarejestruj się, aby zobaczyć notatkę.
To nic nie kosztuje!

Rejestrując się akceptujesz Warunki korzystania z usługi i Politykę prywatności.

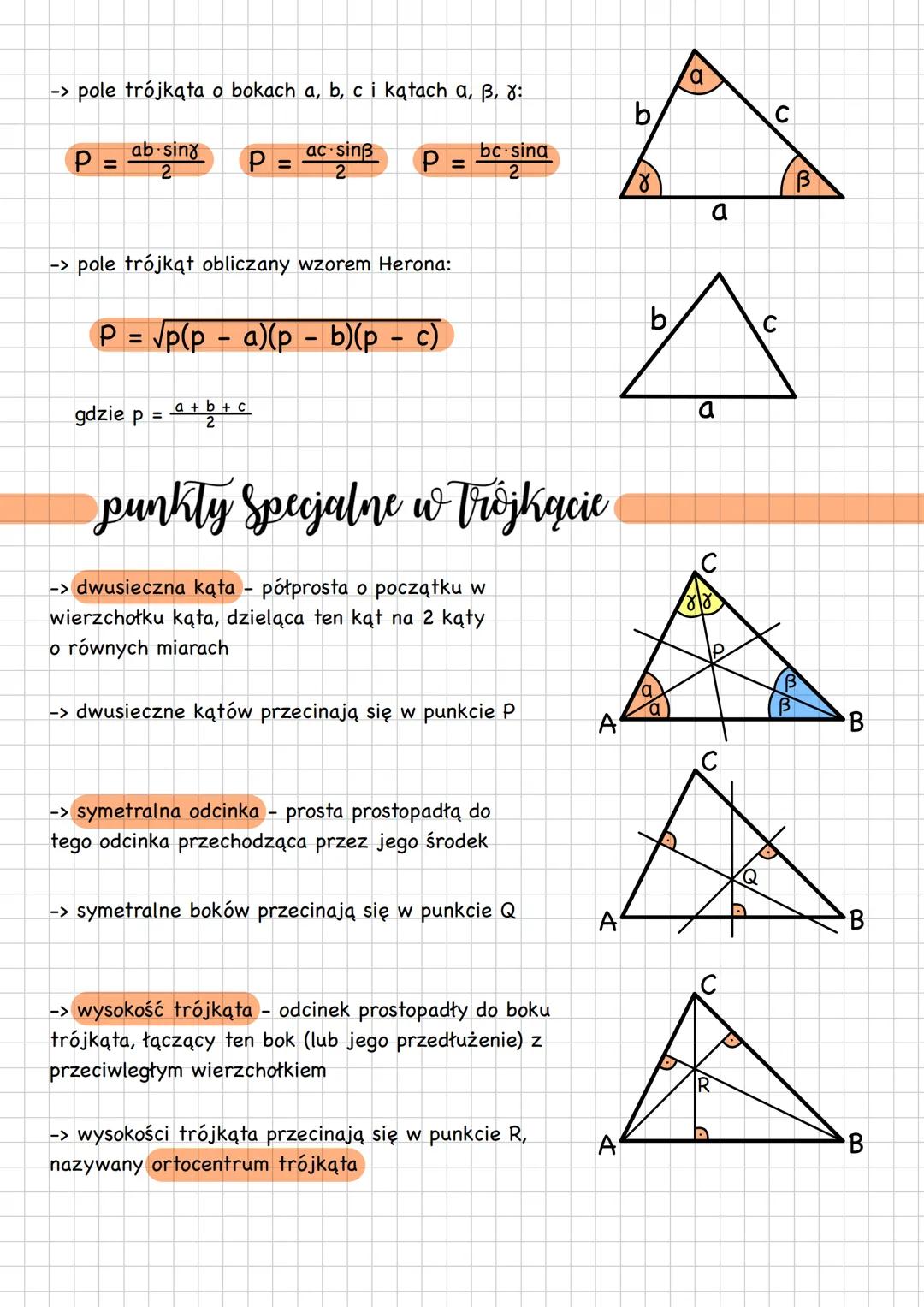
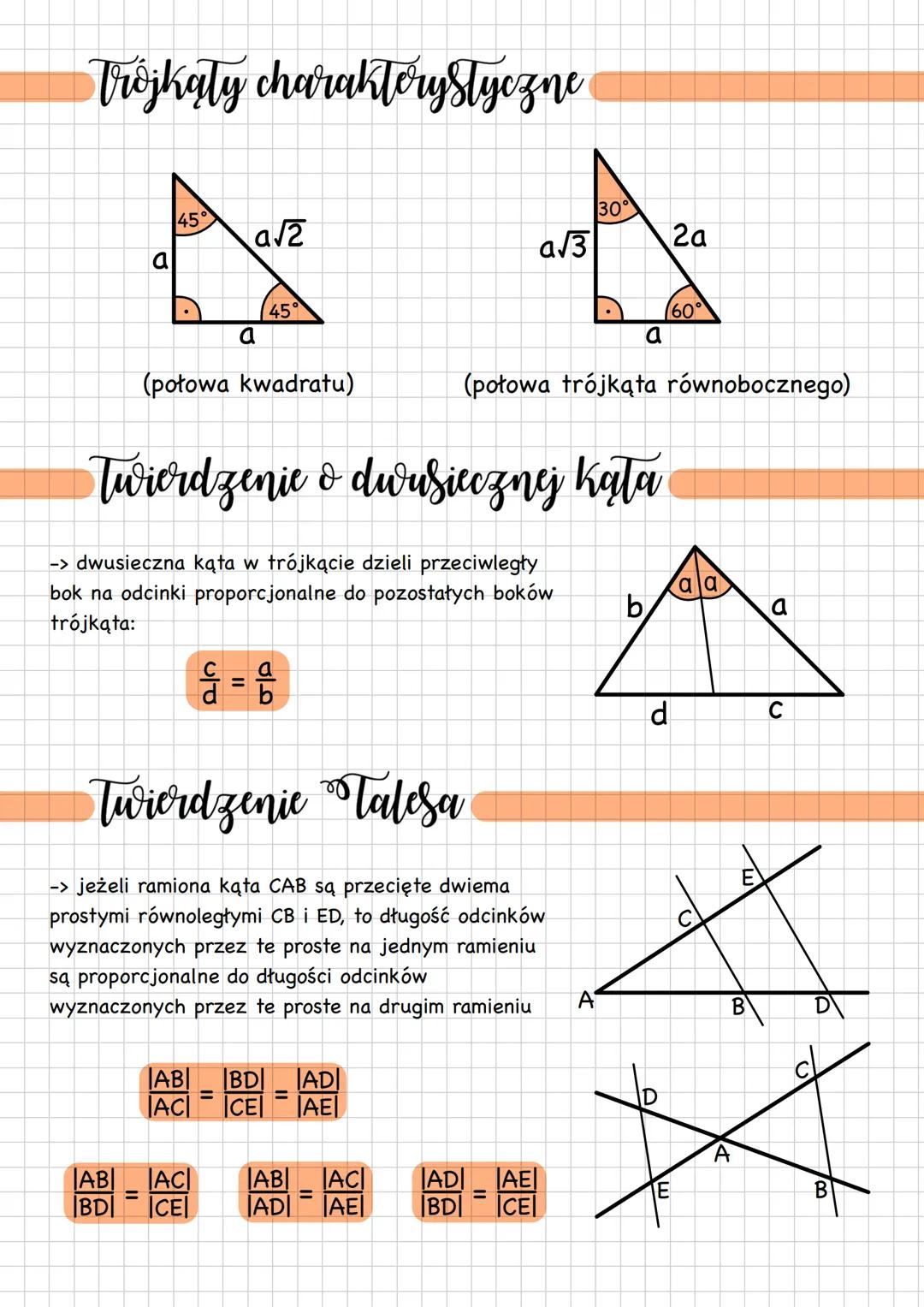
Podstawy trójkątów i ich rodzaje

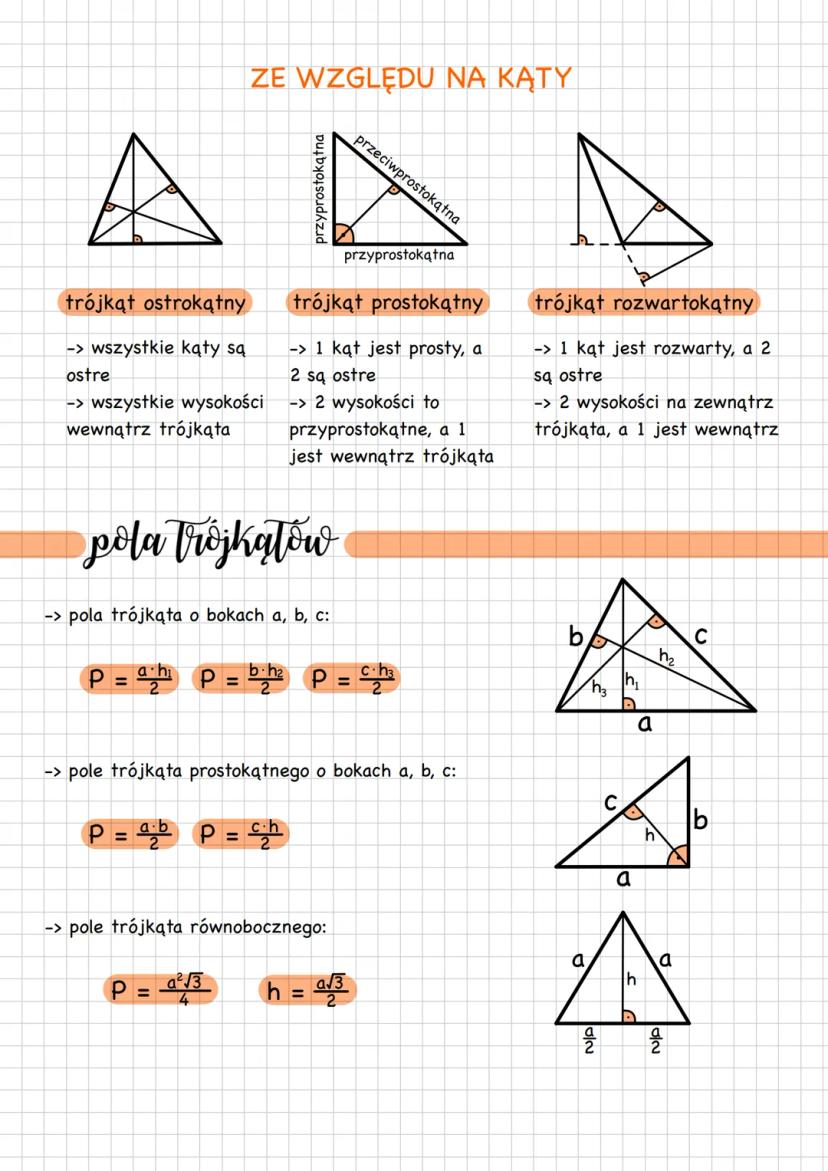
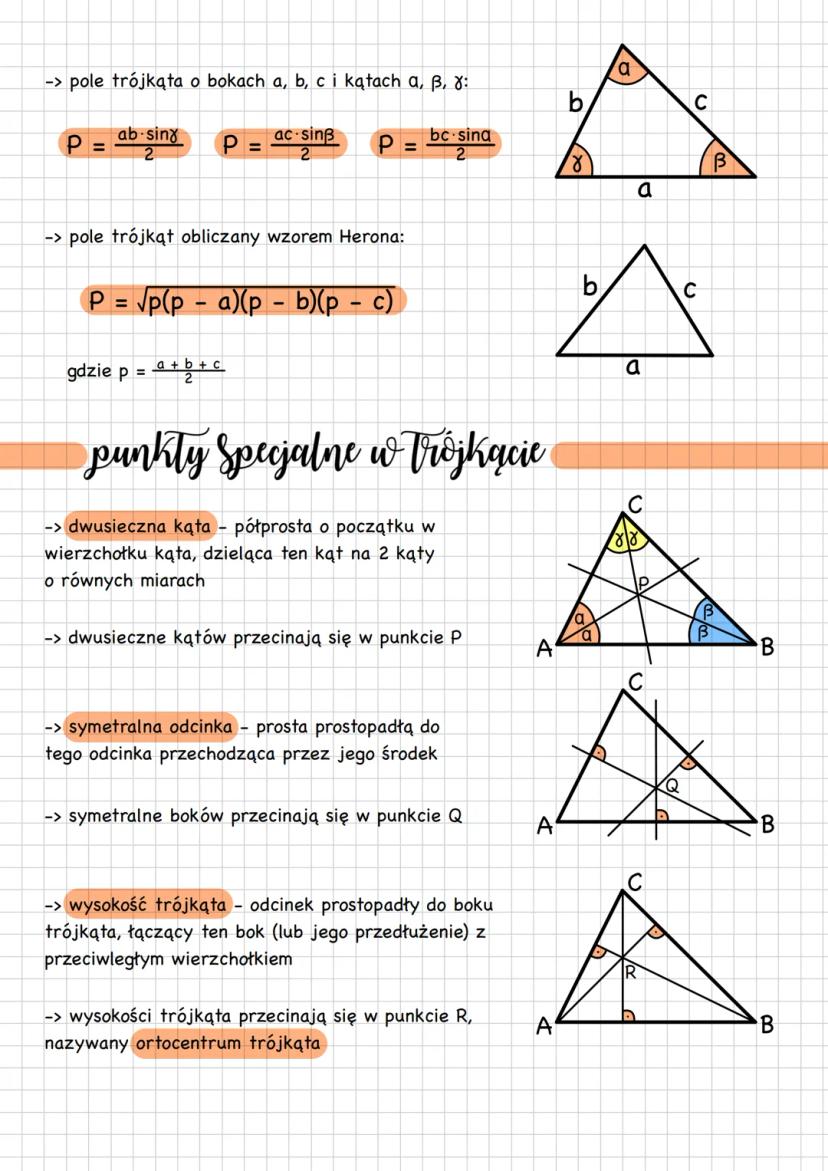
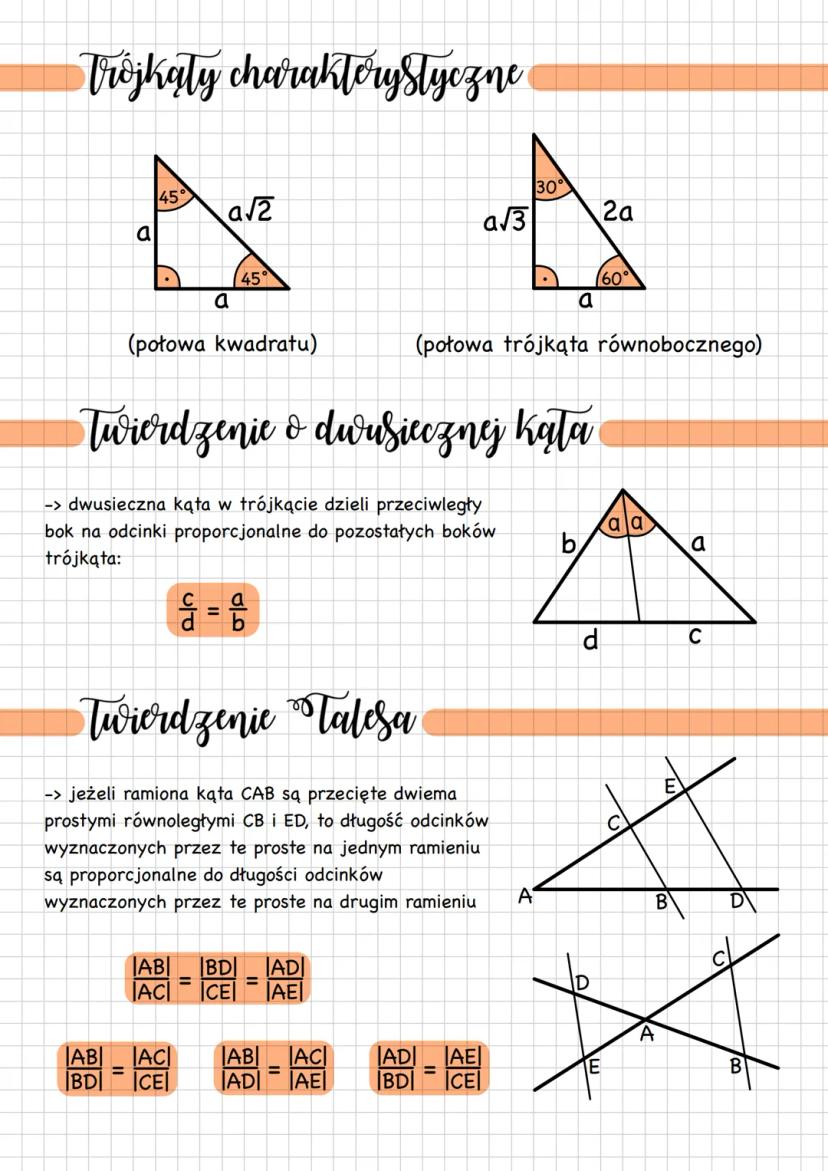
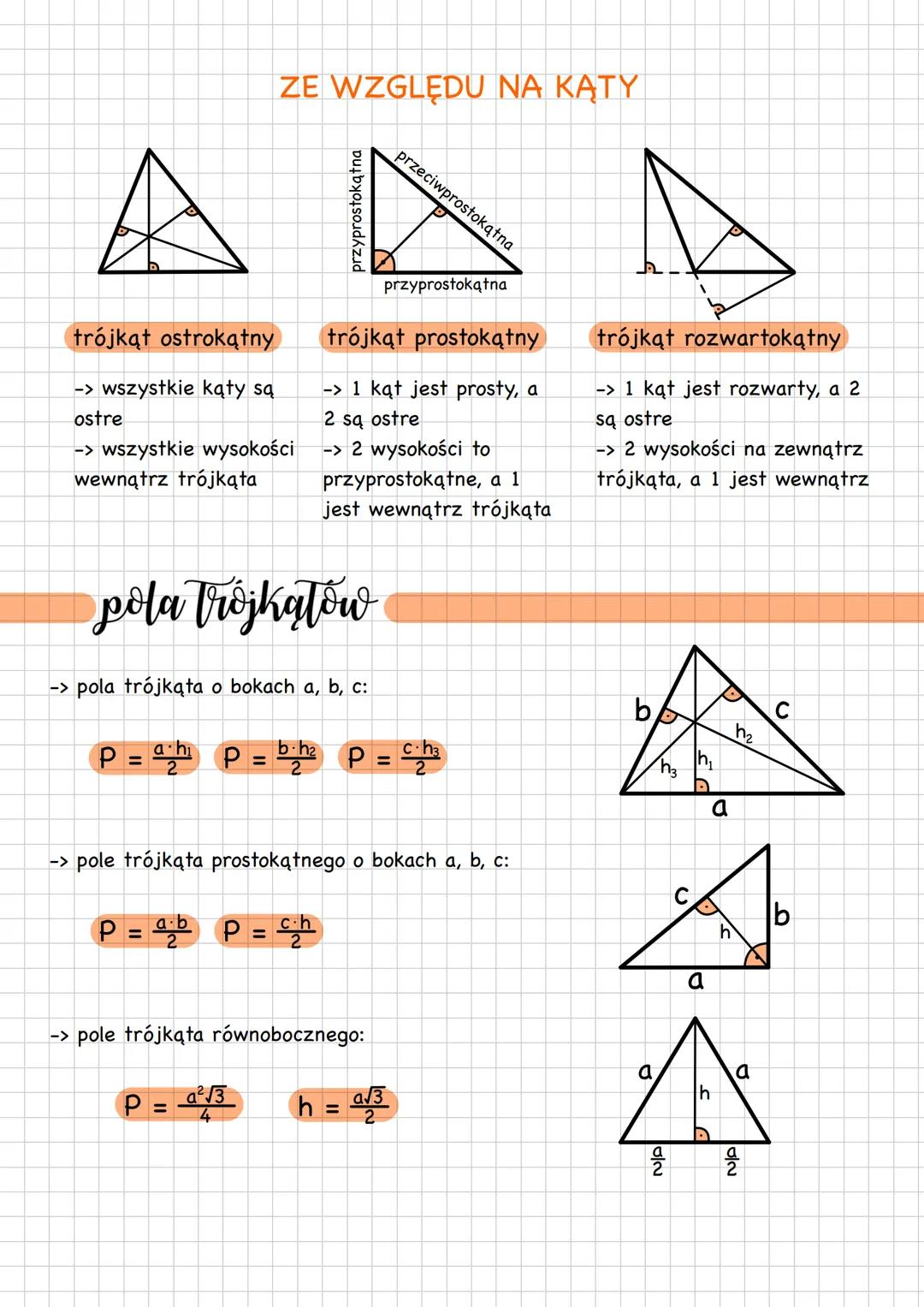
Trójkąt to wielokąt z trzema bokami, trzema wierzchołkami i trzema kątami wewnętrznymi. Najważniejsza zasada? Suma wszystkich kątów w trójkącie zawsze wynosi 180° - to musisz zapamiętać na całe życie!

Żeby w ogóle powstał trójkąt, musi spełniać nierówność trójkąta. Każdy bok musi być krótszy od sumy dwóch pozostałych boków. Sprawdzasz to wzorami: a + b > c, a + c > b, b + c > a.

Ze względu na boki rozróżniamy trzy typy. Trójkąt różnoboczny ma wszystkie boki różnej długości, równoramienny ma dwa równe boki (ramiona) i równe kąty przy podstawie, a równoboczny ma wszystkie boki równe i wszystkie kąty po 60°.

Wskazówka: W trójkącie równoramiennym zawsze zapamiętaj, że kąty przy podstawie są równe!

Trójkąty – strona 2

Zarejestruj się, aby zobaczyć notatkę.
To nic nie kosztuje!

Rejestrując się akceptujesz Warunki korzystania z usługi i Politykę prywatności.

Rodzaje trójkątów ze względu na kąty i obliczanie pól

Ze względu na kąty mamy trzy rodzaje trójkątów. Trójkąt ostrokątny ma wszystkie kąty ostre (mniejsze niż 90°), prostokątny ma jeden kąt prosty (dokładnie 90°), a rozwartokątny ma jeden kąt rozwarty (większy niż 90°).

W trójkącie prostokątnym najdłuższy bok nazywamy przeciwprostokątną, a dwa krótsze to przyprostokątne. To kluczowe pojęcia do twierdzenia Pitagorasa!

Podstawowy wzór na pole trójkąta to P = (a × h)/2, gdzie h to wysokość opuszczona na bok a. Dla trójkąta prostokątnego wystarczy pomnożyć przyprostokątne i podzielić przez 2. Trójkąt równoboczny ma specjalny wzór: P = (a²√3)/4.

Pamiętaj: Pole trójkąta to zawsze połowa iloczynu podstawy i wysokości!

Trójkąty – strona 3

Zarejestruj się, aby zobaczyć notatkę.
To nic nie kosztuje!

Rejestrując się akceptujesz Warunki korzystania z usługi i Politykę prywatności.

Wzory na pole i punkty specjalne

Gdy znasz długości boków i kąty, możesz liczyć pole wzorem P = (ab × sin γ)/2. Jeśli masz tylko długości wszystkich boków, użyj wzoru Herona: P = √p(p−a)(p−b)(p−c)p(p-a)(p-b)(p-c), gdzie p to półobwód trójkąta.

W każdym trójkącie znajdziesz cztery ważne punkty specjalne. Dwusieczne kątów przecinają się w jednym punkcie, symetralne boków też się przecinają w jednym miejscu.

Wysokości trójkąta (odcinki prostopadłe do boków) spotykają się w ortocentrum. Środkowe (łączące wierzchołki ze środkami przeciwległych boków) przecinają się w barycentrum - środku ciężkości trójkąta.

Ciekawostka: Barycentrum dzieli każdą środkową w stosunku 2:1, licząc od wierzchołka!

Trójkąty – strona 4

Zarejestruj się, aby zobaczyć notatkę.
To nic nie kosztuje!

Rejestrując się akceptujesz Warunki korzystania z usługi i Politykę prywatności.

Trójkąty przystające

Trójkąty przystające to takie, które mają dokładnie ten sam kształt i rozmiar - można je na siebie nałożyć. Sprawdzasz to trzema sposobami, zwanymi cechami przystawania.

Cecha BBB (bok-bok-bok): jeśli wszystkie odpowiednie boki są równe, trójkąty są przystające. Cecha BKB (bok-kąt-bok): gdy dwa boki i kąt między nimi są równe. Cecha KBK (kąt-bok-kąt): gdy bok i dwa kąty przy nim są równe.

Te cechy to Twoje narzędzia do dowodzenia w geometrii. Wystarczy sprawdzić jedną z nich, żeby udowodnić przystawanie całych trójkątów.

Wskazówka: W testach najczęściej sprawdzają cechę BKB - zapamiętaj ją jako pierwszą!

Trójkąty – strona 5

Zarejestruj się, aby zobaczyć notatkę.
To nic nie kosztuje!

Rejestrując się akceptujesz Warunki korzystania z usługi i Politykę prywatności.

Trójkąty podobne i twierdzenie Pitagorasa

Trójkąty podobne mają ten sam kształt, ale mogą mieć różne rozmiary. To jak powiększona lub pomniejszona kopia. Sprawdzasz podobieństwo podobnymi cechami jak przy przystawaniu.

Cecha BBB dla podobieństwa: boki są proporcjonalne a/a′=b/b′=c/c′a/a' = b/b' = c/c'. Cecha BKB: dwa boki są proporcjonalne i kąt między nimi jest równy. Cecha KKK: wszystkie odpowiednie kąty są równe.

Twierdzenie Pitagorasa to gwiazda geometrii! W trójkącie prostokątnym: a² + b² = c², gdzie c to przeciwprostokątna. Sprawdza się w każdym trójkącie prostokątnym na świecie.

Pamiętaj: Twierdzenie Pitagorasa działa TYLKO w trójkątach prostokątnych!

Trójkąty – strona 6

Zarejestruj się, aby zobaczyć notatkę.
To nic nie kosztuje!

Rejestrując się akceptujesz Warunki korzystania z usługi i Politykę prywatności.

Trójkąty charakterystyczne i ważne twierdzenia

Dwa trójkąty charakterystyczne musisz znać na pamięć! Trójkąt o kątach 45°-45°-90° (połowa kwadratu) ma boki w stosunku 1:1:√2. Trójkąt 30°-60°-90° (połowa trójkąta równobocznego) ma boki w stosunku 1:√3:2.

Twierdzenie o dwusiecznej mówi, że dwusieczna kąta dzieli przeciwległy bok na odcinki proporcjonalne do pozostałych boków trójkąta. Wzór: a₁/a₂ = b/c.

Twierdzenie Talesa dotyczy prostych równoległych przecinających ramiona kąta. Odcinki na jednym ramieniu są proporcjonalne do odcinków na drugim ramieniu.

Przydatne: Trójkąty charakterystyczne często pojawiają się w zadaniach - warto je narysować i zawiesić nad biurkiem!

Trójkąty – strona 7

Zarejestruj się, aby zobaczyć notatkę.
To nic nie kosztuje!

Rejestrując się akceptujesz Warunki korzystania z usługi i Politykę prywatności.

Twierdzenia sinusów i cosinusów

Twierdzenie sinusów łączy długości boków z sinusami przeciwległych kątów. Wzór: a/sin α = b/sin β = c/sin γ = 2R, gdzie R to promień okręgu opisanego na trójkącie.

Twierdzenie cosinusów to uogólnienie twierdzenia Pitagorasa na wszystkie trójkąty. Najważniejszy wzór: a² = b² + c² - 2bc cos α. Gdy α = 90°, cosinus znika i zostaje zwykły Pitagoras!

Te twierdzenia to Twoja broń na najtrudniejsze zadania z trójkątów. Sinusów używasz, gdy masz kąty i jeden bok. Cosinusów - gdy masz dwa boki i kąt między nimi lub wszystkie boki.

Pro tip: Twierdzenie cosinusów zawsze działa - to Twój plan B, gdy inne metody zawodzą!

Myśleliśmy, że nigdy nie zapytasz...

Nasz asystent AI jest specjalnie dostosowany do potrzeb uczniów. W oparciu o miliony treści, które mamy na platformie, możemy udzielać uczniom naprawdę znaczących i trafnych odpowiedzi. Ale nie chodzi tylko o odpowiedzi, towarzysz prowadzi również uczniów przez codzienne wyzwania związane z nauką, ze spersonalizowanymi planami nauki, quizami lub treściami na czacie i 100% personalizacją opartą na umiejętnościach i rozwoju uczniów.

Aplikację możesz pobrać z Google Play i Apple Store.

Tak, masz całkowicie darmowy dostęp do wszystkich notatek w aplikacji, możesz w każdej chwili rozmawiać z Ekspertami lub ich obserwować. Możesz użyć punktów, aby odblokować pewne funkcje w aplikacji, które również możesz otrzymać za darmo. Dodatkowo oferujemy usługę Knowunity Premium, która pozwala na odblokowanie większej liczby funkcji.

Podobne notatki

Matematyka

Koła i kąty

Teoria na temat kątów i geometrii

28866
Matematyka

Twierdzenie cosinusów

Notatka z lekcji wraz z zadaniami i treścią zadań

42253
Matematyka

Wzory na pole kwadratu i prostokąta

Zrozumienie wzorów na pole kwadratu i prostokąta z przykładami obliczeń. Dowiedz się, jak obliczyć pole kwadratu (P = a²) oraz prostokąta (P = a*b) i zobacz praktyczne zastosowania. Idealne dla uczniów przygotowujących się do egzaminów z matematyki.

5 SP179552
Matematyka

Własności figur geometrycznych

Zgłębiaj własności figur geometrycznych, w tym kwadratu, prostokąta, rombu, równoległoboku i trapezu. Dowiedz się, jak obliczać pola i obwody oraz poznaj kluczowe cechy czworokątów. Idealne dla uczniów przygotowujących się do egzaminów z geometrii.

8 SP181859
Matematyka

Wzory Figur Geometrycznych

Odkryj kluczowe wzory na obwód i pole różnych figur geometrycznych, w tym kwadratów, prostokątów, trójkątów, trapezów i równoległoboków. Idealne dla uczniów przygotowujących się do egzaminów. Zawiera formuły obliczeniowe i przykłady zastosowania.

6 SP270642
Matematyka

Podstawowe figury geometryczne

Zrozum podstawowe figury geometryczne, takie jak kwadrat, prostokąt, trójkąt, romb, prostopadłościan, sześcian i kula. Ta prezentacja dostarcza kluczowych informacji o ich właściwościach i zastosowaniach w geometrii. Idealna dla uczniów przygotowujących się do egzaminów z matematyki.

23944
Zobacz więcej

Najpopularniejsze notatki: twierdzenia geometryczne

Matematyka

Koła i kąty

Teoria na temat kątów i geometrii

28866

Najpopularniejsze notatki: Matematyka

Matematyka

Nwd i nww

Obliczanie i wyjasnienie nww oraz nwd

6 SP499998
Matematyka

Ułamki Dziesiętne: Operacje

Zrozumienie ułamków dziesiętnych: ich zapis, konwersja na ułamki zwykłe oraz podstawowe operacje matematyczne, takie jak dodawanie, odejmowanie, mnożenie i dzielenie. Przykłady i szczegółowe wyjaśnienia dla uczniów. Typ: Podsumowanie.

6 SP22 009649
Matematyka

Analiza Funkcji Kwadratowej

Zrozumienie funkcji kwadratowej, jej właściwości, miejsca zerowe oraz zastosowanie w rozwiązywaniu równań. Materiał obejmuje przykłady, wzory oraz metody analizy funkcji kwadratowej w kontekście geometrii i algebraicznych równań. Typ: Podsumowanie.

172 8743221
Matematyka

Cechy Podzielności Liczb

Zrozum zasady podzielności liczb naturalnych, całkowitych, wymiernych i niewymiernych. Dowiedz się, jak rozpoznawać liczby parzyste i nieparzyste oraz zastosować reguły podzielności w praktyce. Idealne dla uczniów przygotowujących się do egzaminów z matematyki.

7 SP192639
Matematyka

Tabliczka mnożenia od 1 do 100 Klasa 1-4

Tabliczka mnożenia do nauki dla klas 1-4

8 SP378136
Matematyka

Rodzaje Liczb Matematycznych

Odkryj różne rodzaje liczb w matematyce: przeciwne, odwrotne, pierwsze, złożone, naturalne, całkowite, wymierne, niewymierne, rzeczywiste, parzyste i nieparzyste. Zrozum definicje i przykłady dla każdego typu liczby. Idealne dla uczniów przygotowujących się do egzaminów z matematyki.

6 SP7705194
Matematyka

LICZBY NATURALNE

📘 Notatka dotyczy liczb naturalnych. Idealna do szybkiej powtórki przed sprawdzianem lub maturą. Proste wyjaśnienia, uporządkowana teoria i przykłady ułatwiające zrozumienie. #matematyka #liczbyNaturalne #matura #egzamin #wiedza #powtórka

1153329
Matematyka

NWD i NWW: Metody Obliczeń

Zrozumienie i obliczanie NWD (największy wspólny dzielnik) oraz NWW (najmniejsza wspólna wielokrotność) z zastosowaniem różnych metod. Idealne dla uczniów przygotowujących się do egzaminów z matematyki. Obejmuje przykłady i praktyczne zadania.

7 SP27 3431726
Matematyka

Funkcja liniowa

Zakres podstawowy

1104525

Najpopularniejsze notatki

Biologia

Budowa i funkcje skóry

Szczegółowa notatka z biologii dla klas 7, podręcznik wydawnictwa nowej ery - Puls życia. Temat: Budowa i funkcje skóry.

7 SP6242190
Język polski

Inny Świat: Wspomnienia z Jercewa

Odkryj 'Inny Świat' Gustawa Herlinga-Grudzińskiego, autobiograficzną powieść dokumentalną, która ukazuje brutalne realia życia w radzieckim obozie pracy. Autor, oskarżony o szpiegostwo, dzieli się swoimi przeżyciami, refleksjami na temat ludzkiej psychiki oraz relacjami z innymi więźniami. Poznaj głębokie analizy moralności, cierpienia i nadziei w nieludzkich warunkach. Idealne dla studentów literatury i historii, którzy pragną zrozumieć kontekst wojenny i totalitarny.

313 342307
Język polski

Antyk / Starożytność

ramy czasowe, cywilizację, sztuka antyczna, cechy literatury, szkoły filozoficzne, filozofowie, wzorce osobowe, budowa teatru, budowa tragedii antycznej i jej cechy

110 388190
Język angielski

Czasy w Języku Angielskim

Kompleksowe notatki dotyczące podstawowych czasów w języku angielskim, idealne dla maturzystów 2025. Zawierają szczegółowe omówienie Present Simple, Present Continuous, Past Simple, Past Perfect i innych, z przykładami i zasadami użycia. Przygotuj się skutecznie do egzaminu z tym 46-stronicowym materiałem!

423 7891219
Język polski

Mity Greckie: Kluczowe Opowieści

Zanurz się w fascynujący świat mitologii greckiej. Odkryj kluczowe mity, takie jak historia Prometeusza, Demeter i Persefony, oraz Syzyfa. Poznaj bogów, herosów i ich niezwykłe przygody, które kształtowały wierzenia starożytnych Greków. Idealne dla studentów literatury i mitologii.

135 7521182
Język polski

Edelman i Powstanie w Getcie

Analiza lektury 'Zdążyć przed Panem Bogiem' Hanny Krall, koncentrująca się na tematach takich jak etyka, cierpienie, oraz heroizm w kontekście powstania w warszawskim getcie. Opracowanie omawia genezę, problematykę oraz kluczowe postacie, w tym Marka Edelmana, ukazując złożoność wyborów moralnych w obliczu Holokaustu.

312 887301
Język polski

Walka o Godność w Getcie

Analiza 'Zdążyć przed Panem Bogiem' Hanny Krall, koncentrująca się na powstaniu w warszawskim getcie oraz dążeniu do godnej śmierci. Obejmuje kluczowe wydarzenia, postacie oraz filozoficzne refleksje dotyczące ludzkiej motywacji i cierpienia. Typ: reportaż.

1113 4255270
Język angielski

Czasy w języku angielskim na egzamin ósmoklasisty.

Wszystkie czasy na egzamin ósmoklasisty z języka angielskiego (2025)!<3

8 SP12 383334
Język polski

Części Mowy: Odmienne i Nieodmienne

Zrozumienie części mowy w języku polskim: szczegółowe omówienie odmiennej (rzeczownik, przymiotnik, czasownik, liczebnik, zaimek) oraz nieodmiennej (przysłówek, spójnik, przyimek, partykuła, wykrzyknik) części mowy. Idealne dla uczniów przygotowujących się do egzaminów lub chcących pogłębić wiedzę o gramatyce.

6 SP31 9311241

Zobacz, co mówią o nas nasi użytkownicy. Pokochali nas, pokochasz też i Ty.

4.6/5App Store
4.7/5Google Play
Stefan Sużytkownik iOS

Aplikacja jest bardzo prosta i dobrze przemyślana. Do tej pory znalazłem wszystko, czego szukałem i mogłem się wiele nauczyć z innych notatek! Na pewno wykorzystam aplikację do pomocy przy robieniu prac domowych! No i oczywiście bardzo pomaga też jako inspiracja do robienia swoich notatek.

Samantha Klichużytkownik Androida

Ta aplikacja jest naprawdę świetna. Jest tak wiele notatek i pomocnych informacji [...]. Moim problematycznym przedmiotem jest język niemiecki, a w aplikacji jest w czym wybierać. Dzięki tej aplikacji poprawiłam swój niemiecki. Polecam ją każdemu.

Annaużytkownik iOS

Wow, jestem w szoku. Właśnie wypróbowałam aplikację, ponieważ widziałam ją kilka razy reklamowaną na TikToku jestem absolutnie w szoku. Ta aplikacja jest POMOCĄ, której potrzebujesz w szkole i przede wszystkim oferuje tak wiele rzeczy jak notatki czy streszczenia, które są BARDZO pomocne w moim przypadku.