Twierdzenie sinusów i cosinusów
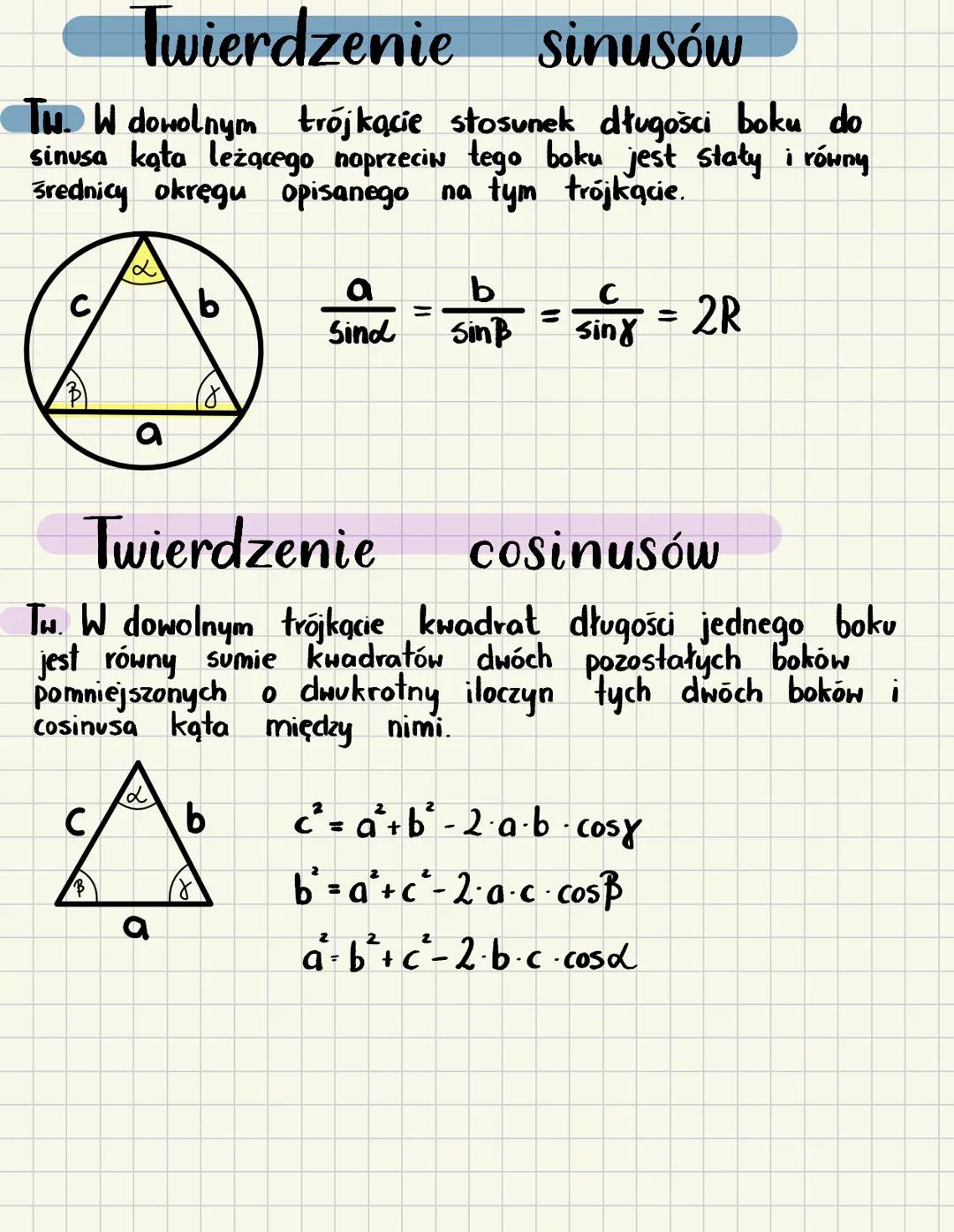
Twierdzenie sinusów mówi, że w dowolnym trójkącie stosunek długości boku do sinusa kąta naprzeciwległego jest stały. Ten stosunek jest równy średnicy okręgu opisanego na trójkącie. Możemy to zapisać jako:
\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2R
Gdzie a, b, c to długości boków, α, β, γ to kąty naprzeciwko tych boków, a R to promień okręgu opisanego na trójkącie.
Twierdzenie cosinusów pozwala nam znaleźć bok trójkąta, gdy znamy dwa pozostałe boki i kąt między nimi. Możemy je zapisać na trzy równoważne sposoby:
c^2 = a^2 + b^2 - 2ab\cos\gamma
b^2 = a^2 + c^2 - 2ac\cos\beta
a^2 = b^2 + c^2 - 2bc\cos\alpha
Wskazówka: Twierdzenie cosinusów jest uogólnieniem twierdzenia Pitagorasa! Jeśli kąt wynosi 90°, cos(90°) = 0, a wzór upraszcza się do znanego c² = a² + b².