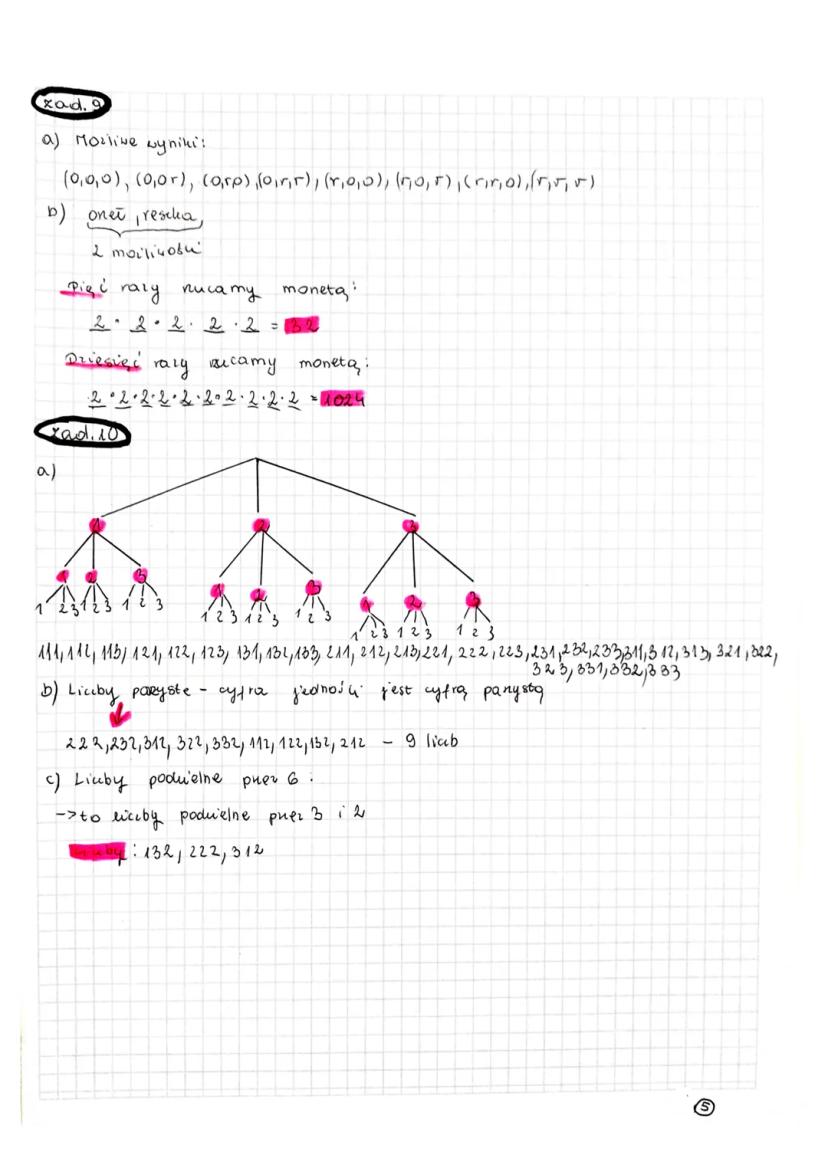
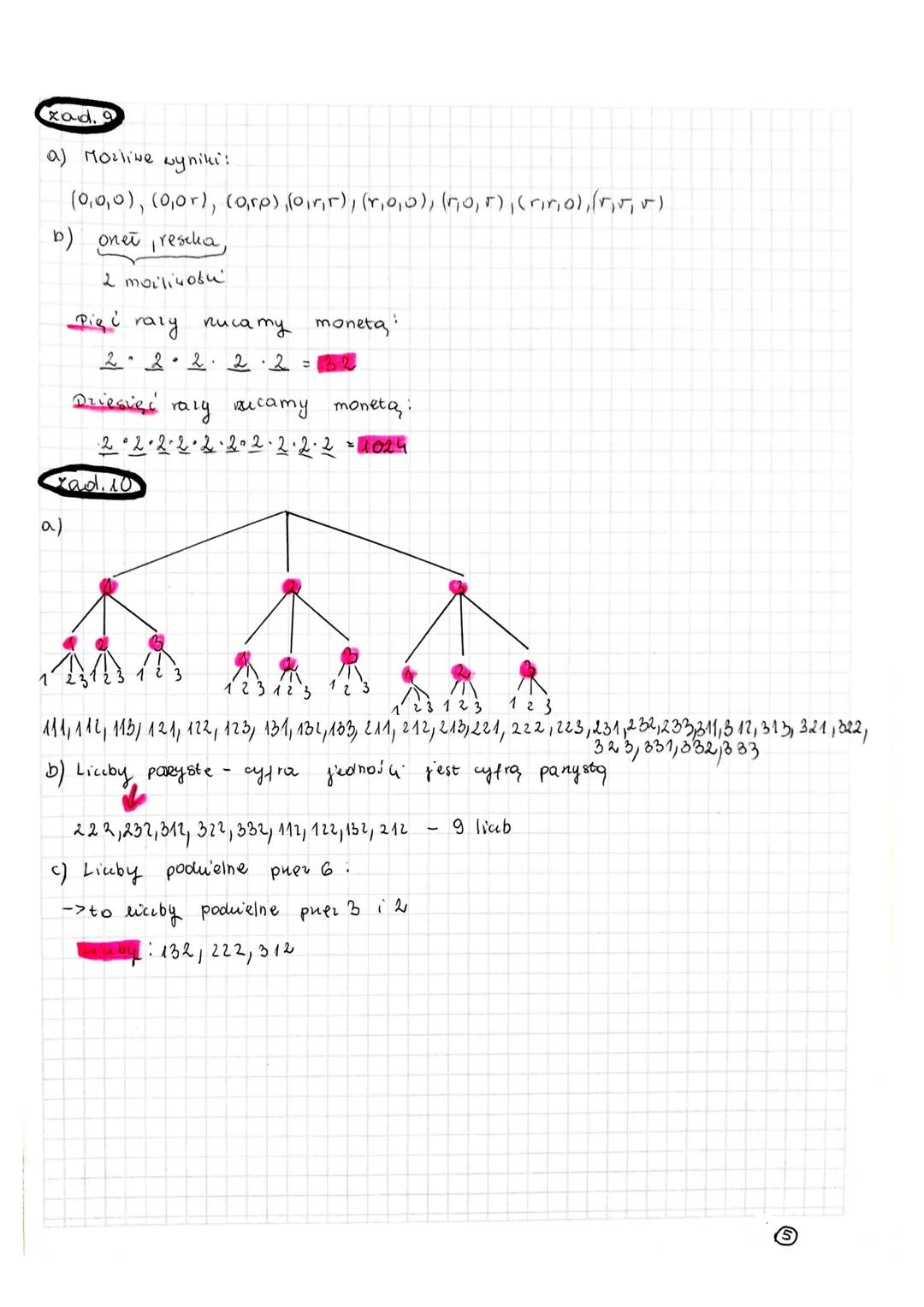
Regula mnożenia to fundamentalne narzędzie kombinatoryki, które pozwala obliczać liczbę... Pokaż więcej
Zarejestruj się, aby zobaczyć notatkęTo nic nie kosztuje!
Dostęp do wszystkich materiałów
Popraw swoje oceny
Dołącz do milionów studentów
Rejestrując się akceptujesz Warunki korzystania z usługi i Politykę prywatności.