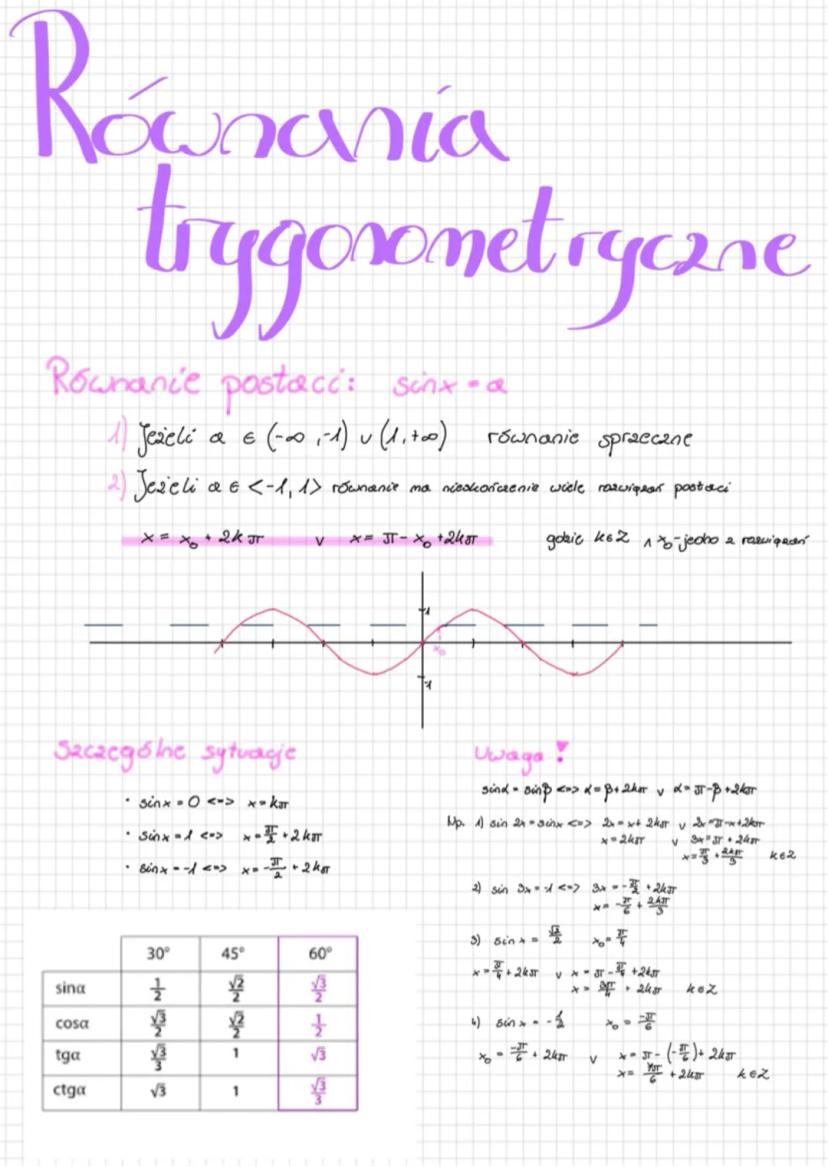
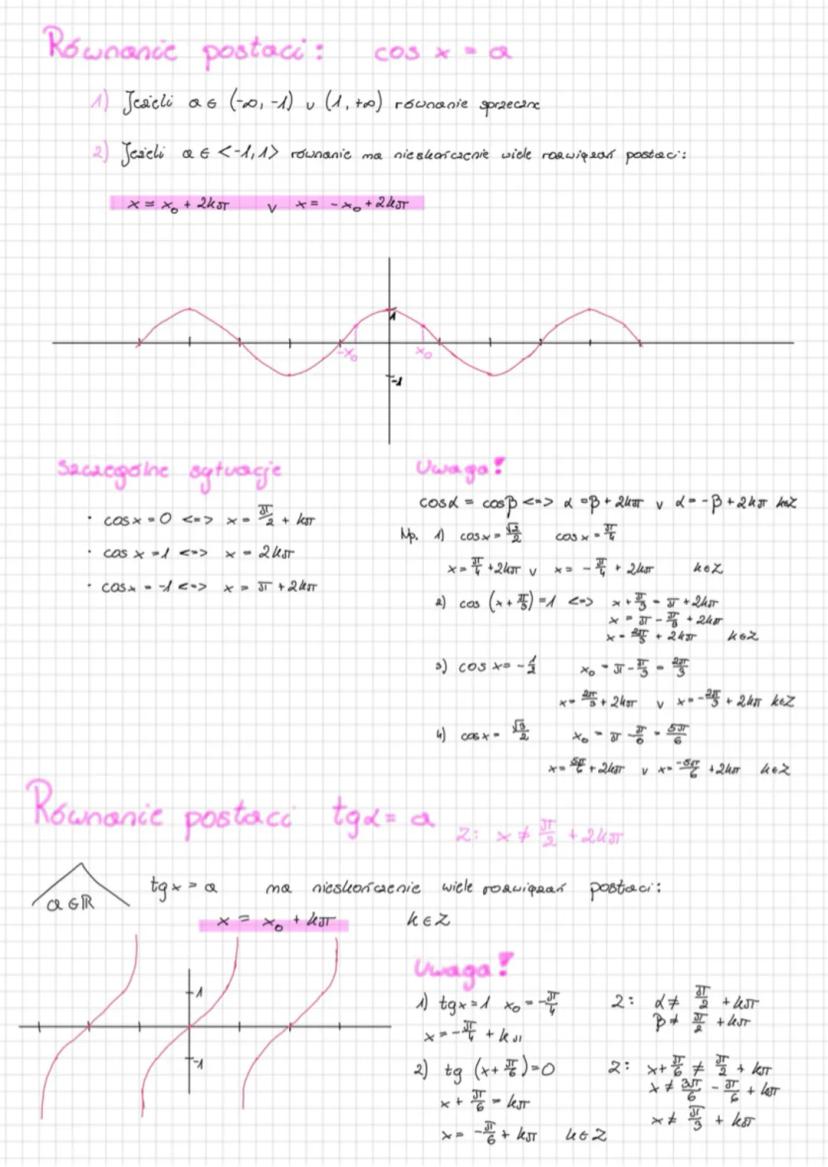
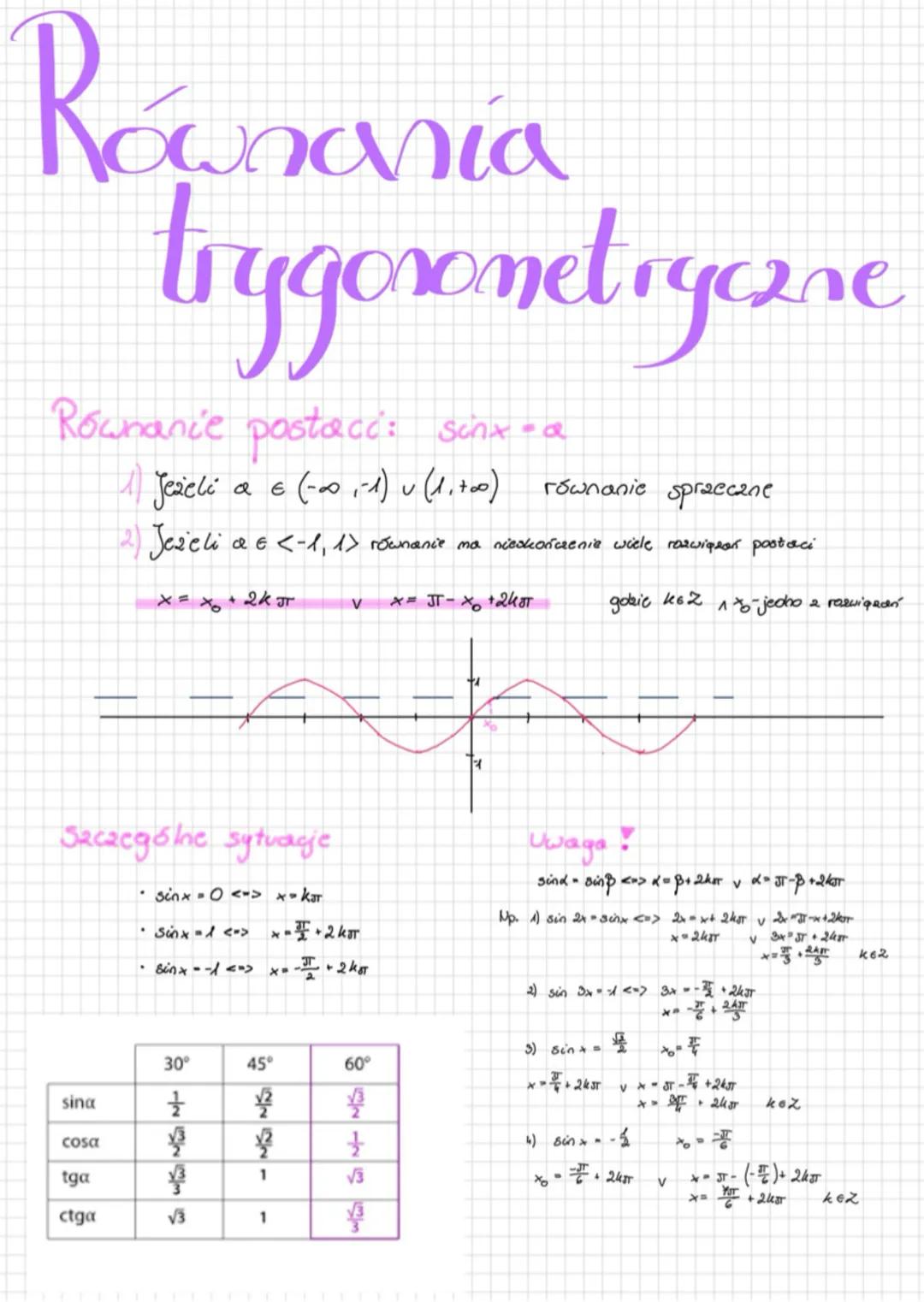
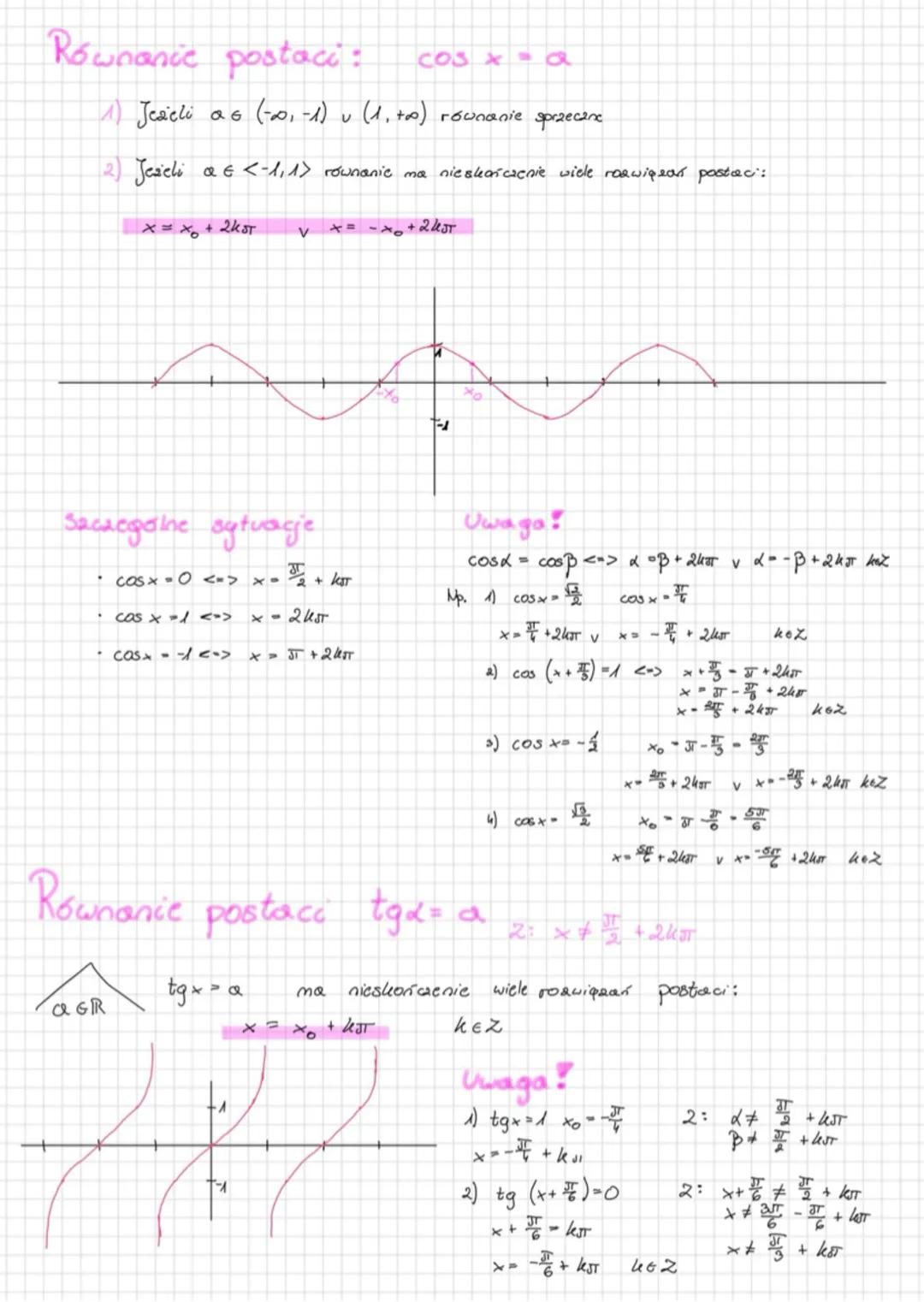
Wzory na sumy i różnice kątów
Zapamiętaj te wzory - to klucz do sukcesu w trygonometrii! Suma kątów ma swoje specjalne wzory: sin(α+β) = sinα·cosβ + sinβ·cosα, a cos(α+β) = cosα·cosβ - sinα·sinβ.
Dla różnicy kątów zmienia się tylko jeden znak: sin(α-β) = sinα·cosβ - sinβ·cosα, cos(α-β) = cosα·cosβ + sinα·sinβ. Wzór na tangens sumy: tg(α+β) = tgα+tgβ/1−tgα⋅tgβ, a dla różnicy w mianowniku mamy plus.
Przykład pokazuje, jak sprytnie używać tych wzorów. Wyrażenie sin24°·cos29° - cos61°·sin45° można przekształcić używając wzorów redukcyjnych, a potem zastosować wzór na sinus sumy kątów, otrzymując ostatecznie wynik -1.
Wskazówka: Zawsze sprawdź, czy można użyć wzorów redukcyjnych przed zastosowaniem wzorów na sumę lub różnicę - często znacznie upraszcza to obliczenia!