Matematyka

Wyrażenia wymierne i pierwiastki

funkcja wymierna

Matematyka635 wyświetleń·Zaktualizowano 22 sie 2026·6 strony

Funkcja Homograficzna – Wyjaśnienie i Zastosowania

Paulina Paulina@paulinapaulina_urhi

Dodaj do źródeł Google

Funkcja homograficzna to jeden z najważniejszych typów funkcji matematycznych, który...

1 / 6

of 6

Podstawowa funkcja homograficzna

Funkcja homograficzna w najprostszej postaci to $f(x) = \frac{a}{x}$ , gdzie $x \neq 0$ . To znacznie prostsze niż funkcje kwadratowe, ale ma swoje charakterystyczne cechy.

Najważniejsze właściwości takiej funkcji to asymptoty - linie, do których wykres się zbliża, ale ich nie przecina. Asymptota pionowa to oś OY $x = 0$ , a asymptota pozioma to oś OX $y = 0$ .

Dla przykładu $f(x) = \frac{2}{x}$ dziedziną jest $\mathbb{R} \setminus \{0\}$ (wszystkie liczby rzeczywiste oprócz zera), a zbiorem wartości też $\mathbb{R} \setminus \{0\}$ . Funkcja ta nie ma miejsc zerowych i jest malejąca na całej dziedzinie.

Pamiętaj: Funkcja homograficzna nigdy nie przechodzi przez punkt (0,0)!

of 6

Przesuwanie wykresu funkcji

Wykres funkcji można przesuwać używając wzoru $g(x) = f(x-p) + q$ , gdzie wektor przesunięcia to $[p, q]$ . Brzmi skomplikowanie, ale to naprawdę proste!

Jeśli masz $g(x) = \frac{2}{x-2}$ , to przesuwasz wykres o wektor $[2, 0]$ - czyli 2 jednostki w prawo. Asymptota pionowa przesuwa się razem z wykresem na x = 2.

Przesunięcie o wektor $[0, -3]$ daje $g(x) = \frac{2}{x} - 3$ . Teraz asymptota pozioma znajduje się na y = -3 zamiast na y = 0.

Wskazówka: Współrzędne asymptot zawsze pokazują, o ile przesunąłeś wykres!

of 6

Postać kanoniczna i ogólna definicja

Postać kanoniczna funkcji homograficznej to $g(x) = \frac{a}{x-p} + q$ . Tutaj od razu widzisz asymptoty: pionową x = p i poziomą y = q.

Gdy przesuwasz wykres $y = \frac{a}{x}$ o wektor $[p, q]$ , otrzymujesz funkcję $y = \frac{a}{x-p} + q$ . Dziedziną jest $\mathbb{R} \setminus \{p\}$ , a zbiorem wartości $\mathbb{R} \setminus \{q\}$ .

Funkcją homograficzną w pełnej postaci nazywamy $y = \frac{ax+b}{cx+d}$ , gdzie $c \neq 0$ i $ad-bc \neq 0$ . Te warunki zapewniają, że funkcja rzeczywiście jest homograficzna.

Ważne: Zawsze sprawdzaj warunki dla współczynników - bez nich funkcja może nie istnieć!

of 6

Rozwiązywanie zadań praktycznych

Zobaczmy typowe zadanie: wykres $y = \frac{3}{x}$ przesunięto o 2 jednostki w górę. Otrzymujesz $f(x) = \frac{3}{x} + 2$ .

Zbiór wartości to $\mathbb{R} \setminus \{2\}$ , bo asymptota pozioma znajduje się na y = 2. Żeby znaleźć miejsce zerowe, rozwiązujesz równanie $0 = \frac{3}{x} + 2$ .

Przekształcasz: $-2 = \frac{3}{x}$ , więc $x = -\frac{3}{2}$ . Dla wartości funkcji równej 5 masz $5 = \frac{3}{x} + 2$ , skąd $x = 1$ .

Trick: Miejsca zerowe funkcji homograficznej zawsze znajdziesz, przyrównując licznik do zera!

of 6

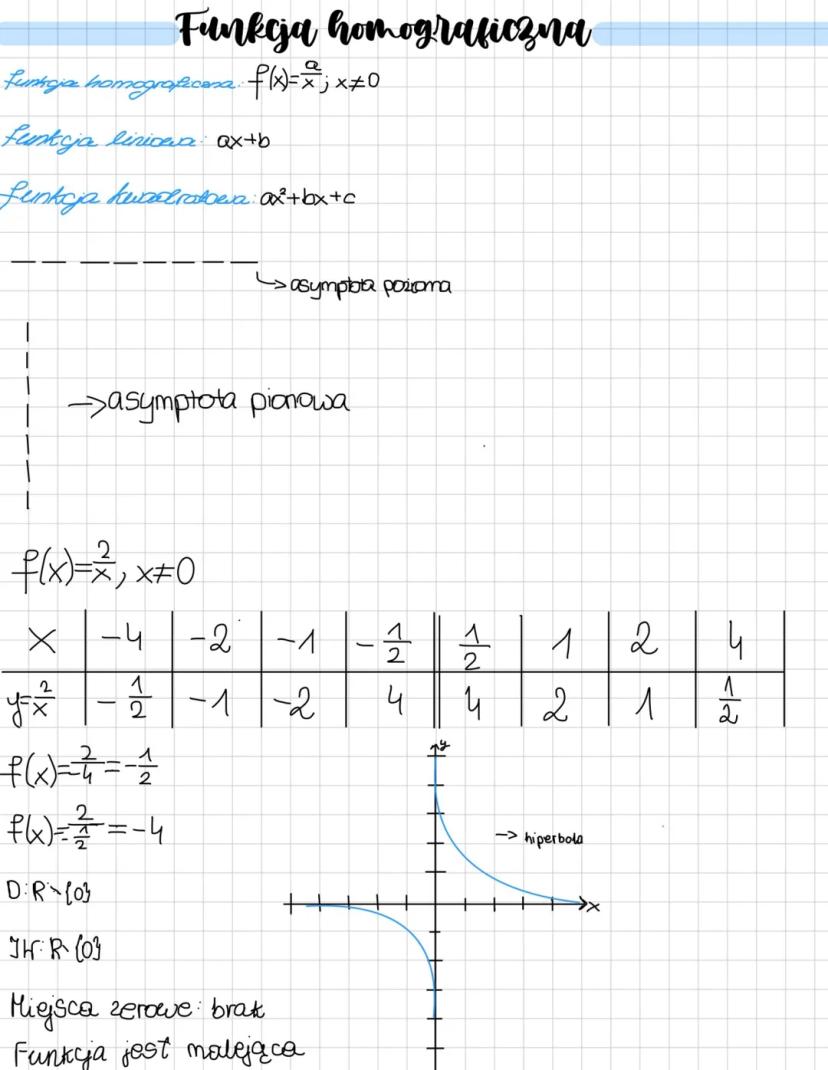
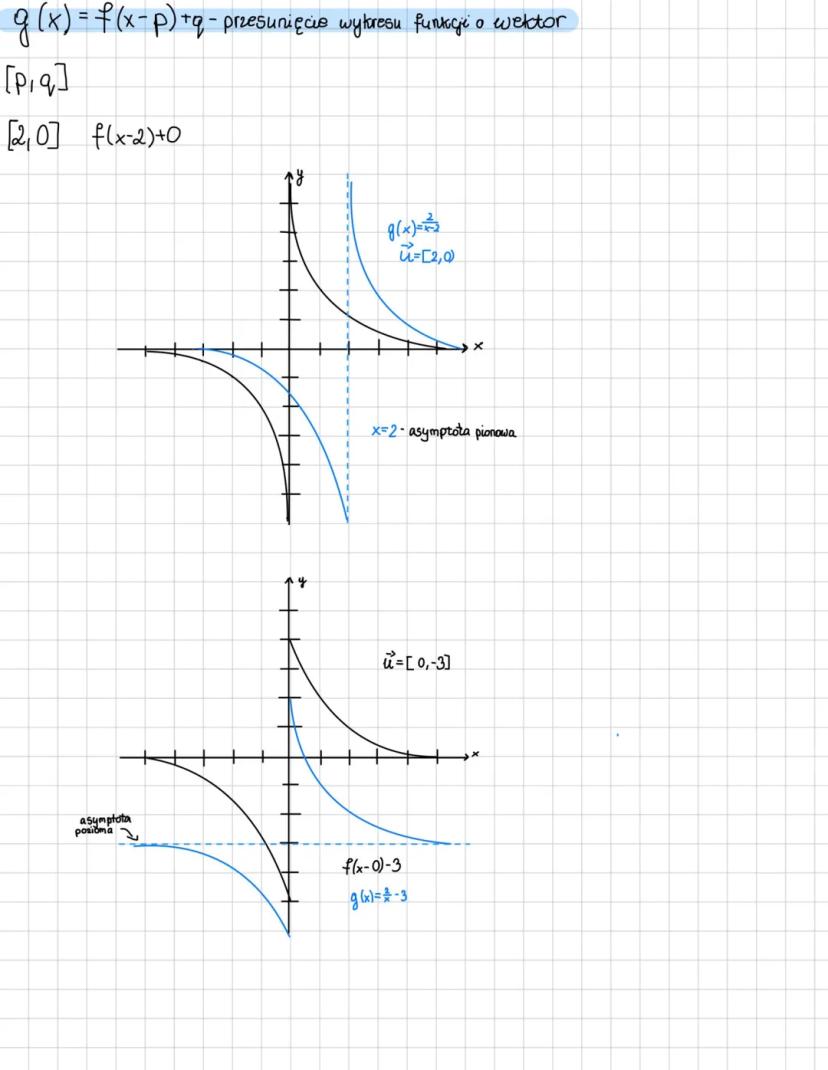
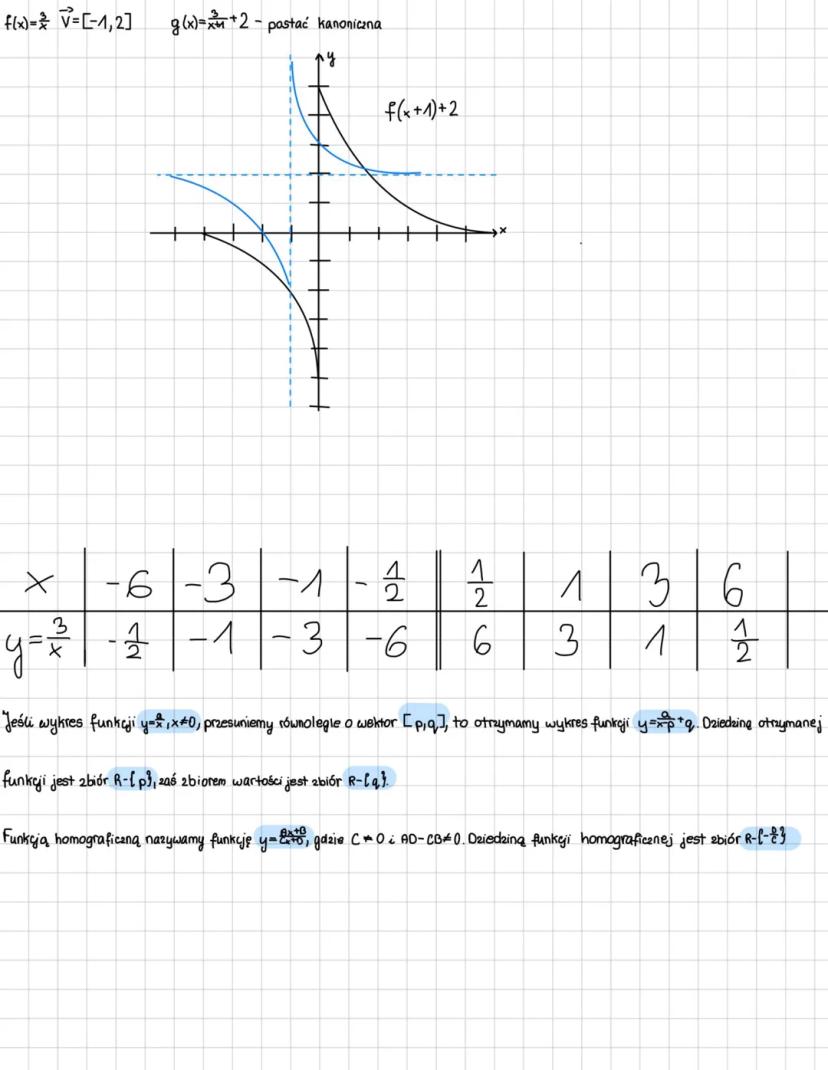
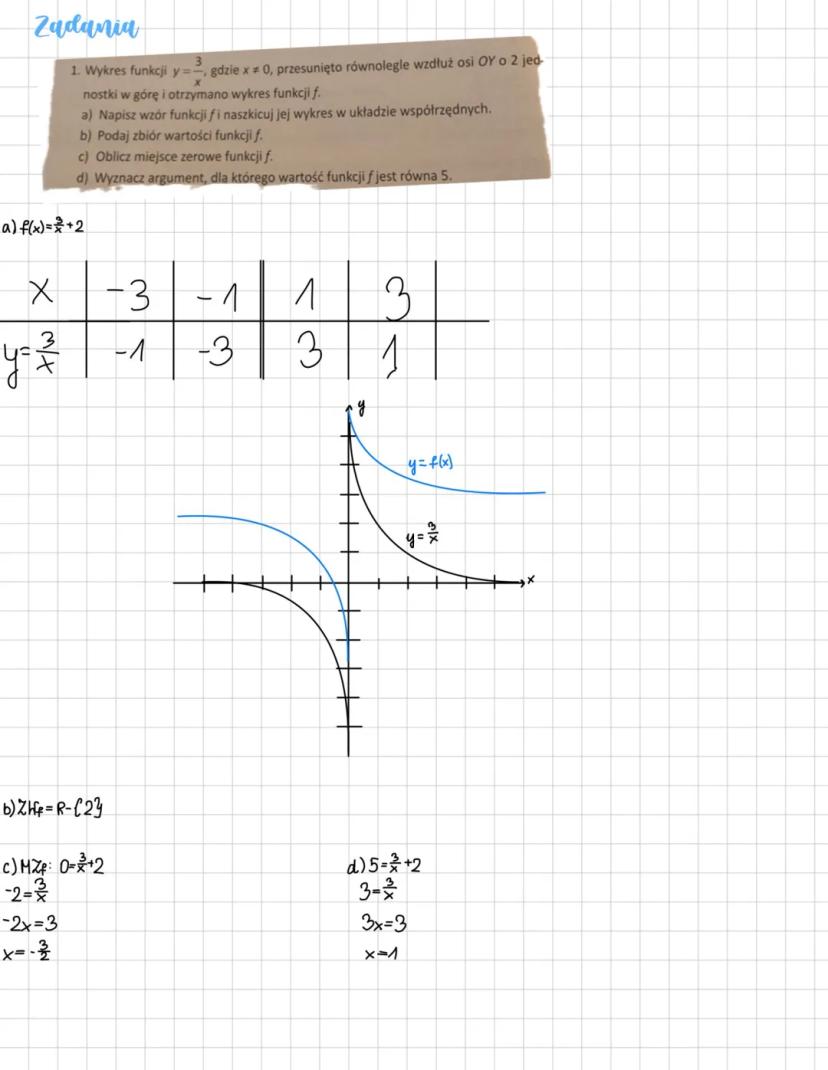
Analiza wykresów i przekształcenia

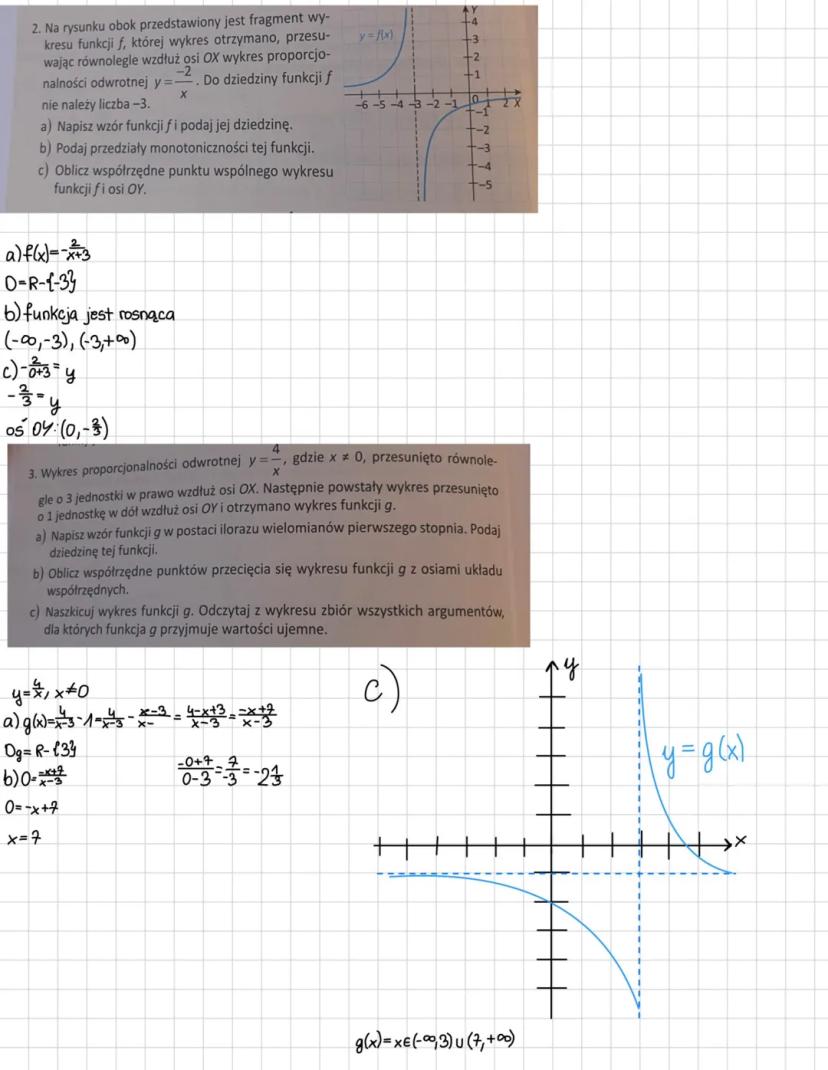
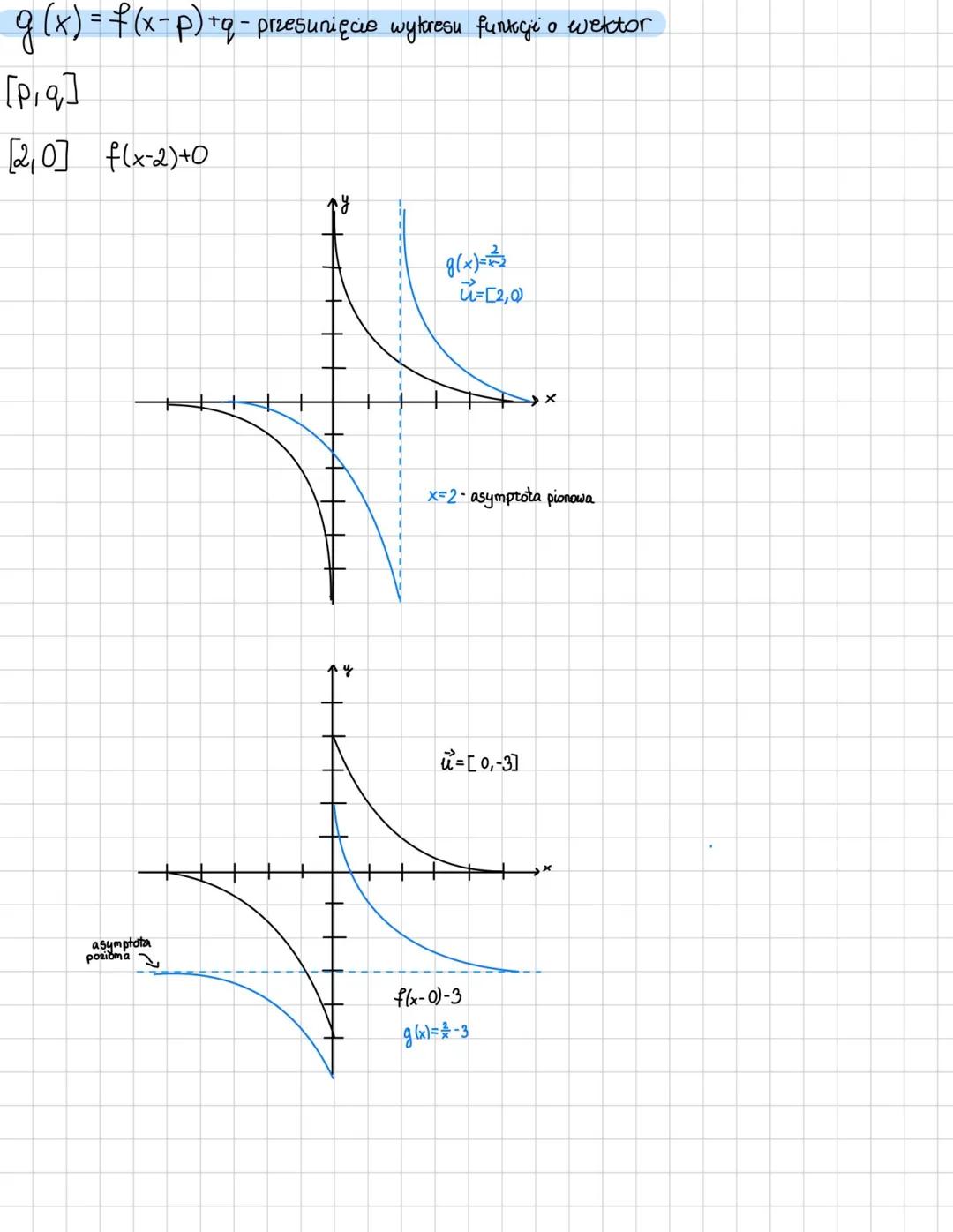
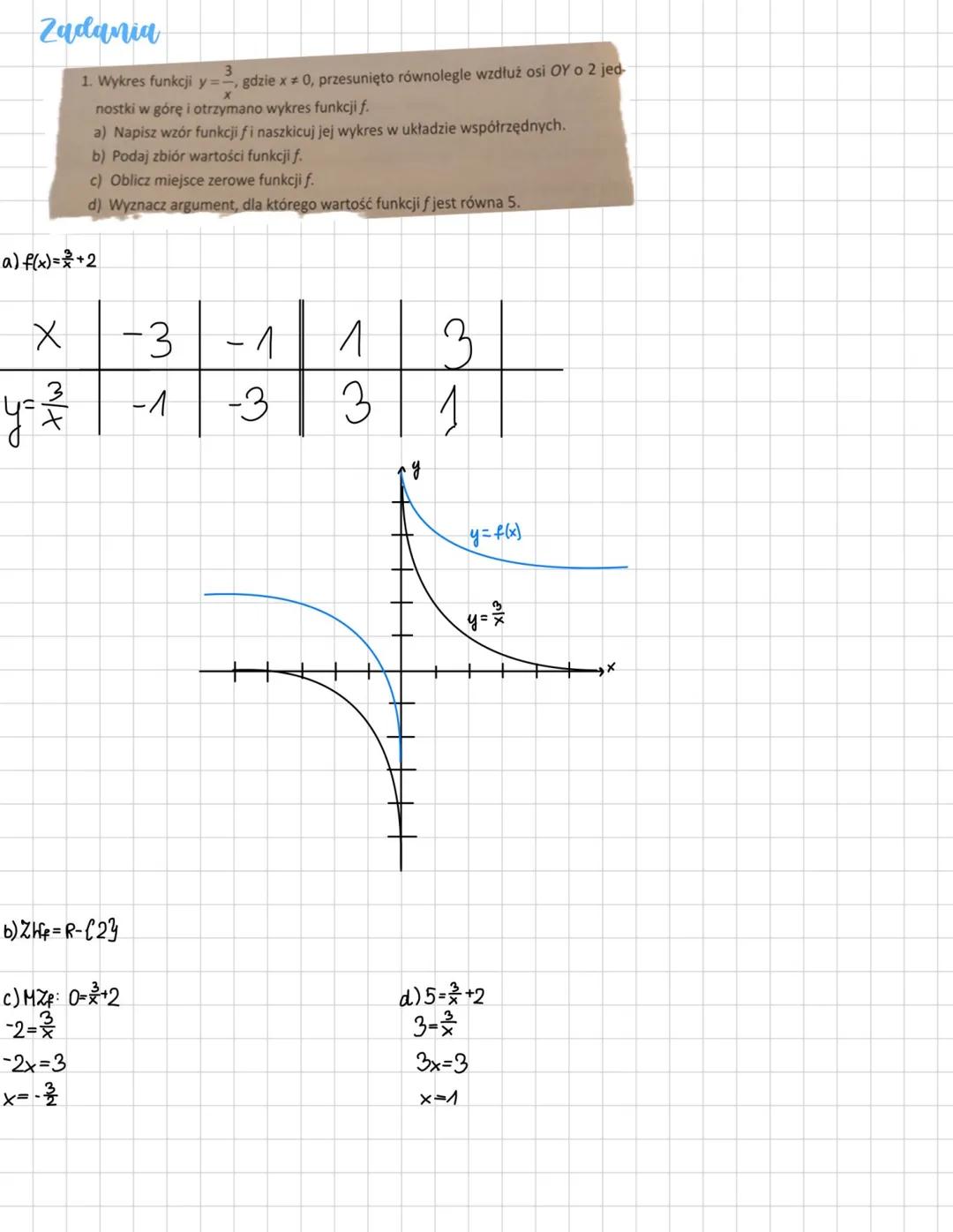
Jeśli wykres $y = \frac{4}{x}$ przesuniesz o 3 jednostki w lewo, otrzymasz $f(x) = \frac{4}{x+3}$ . Dziedzina to $\mathbb{R} \setminus \{-3\}$ , bo asymptota pionowa jest na x = -3.

Funkcja jest malejąca na przedziałach $(-∞, -3)$ i $(-3, ∞)$ . Punkt przecięcia z osią OY znajdziesz, podstawiając x = 0: otrzymujesz $(0, \frac{4}{3})$ .

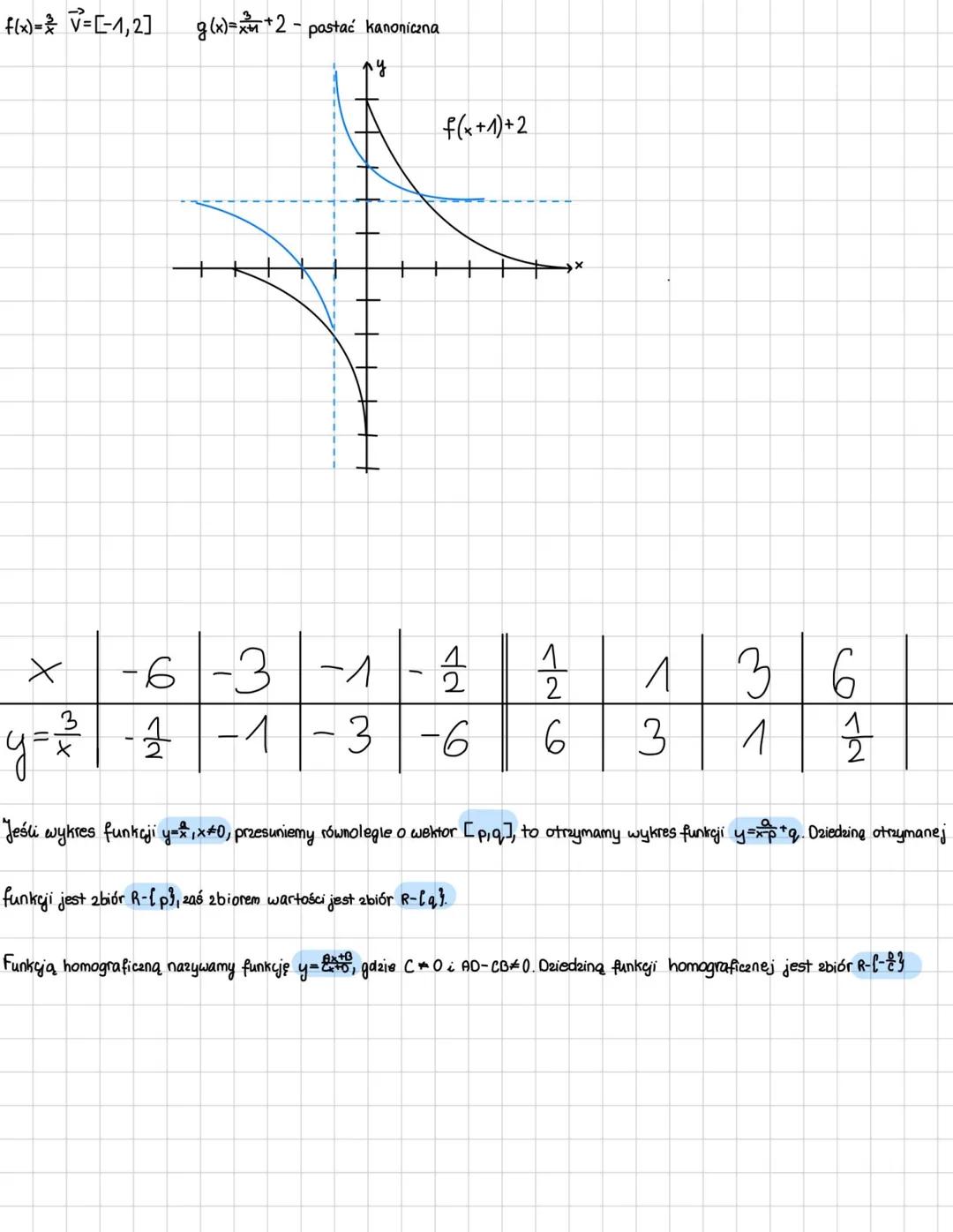
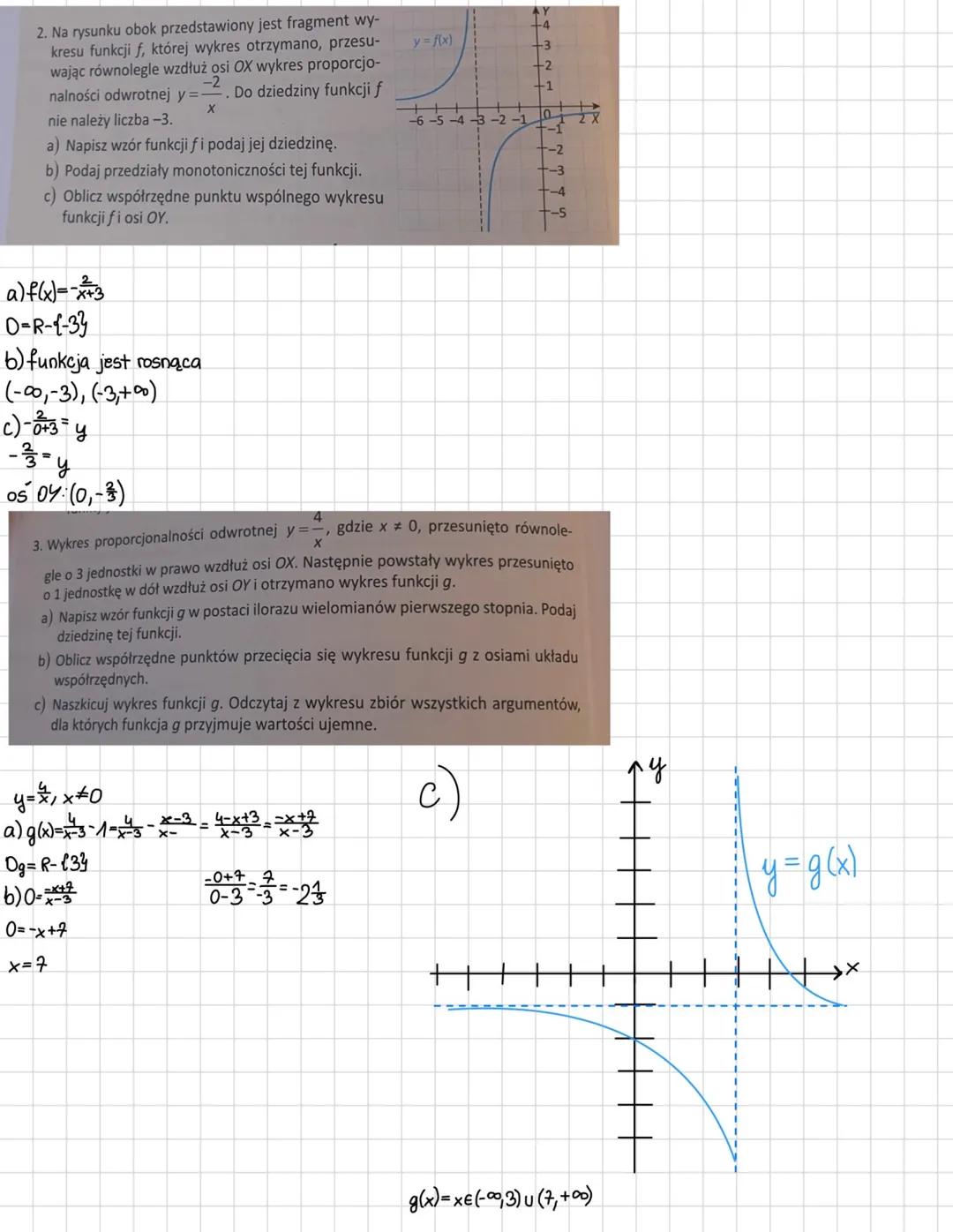
Złożone przekształcenia robisz krok po kroku. Przykład: $y = \frac{4}{x}$ → prawo o 3 → dół o 1 daje $g(x) = \frac{4}{x-3} - 1 = \frac{7-x}{x-3}$ .

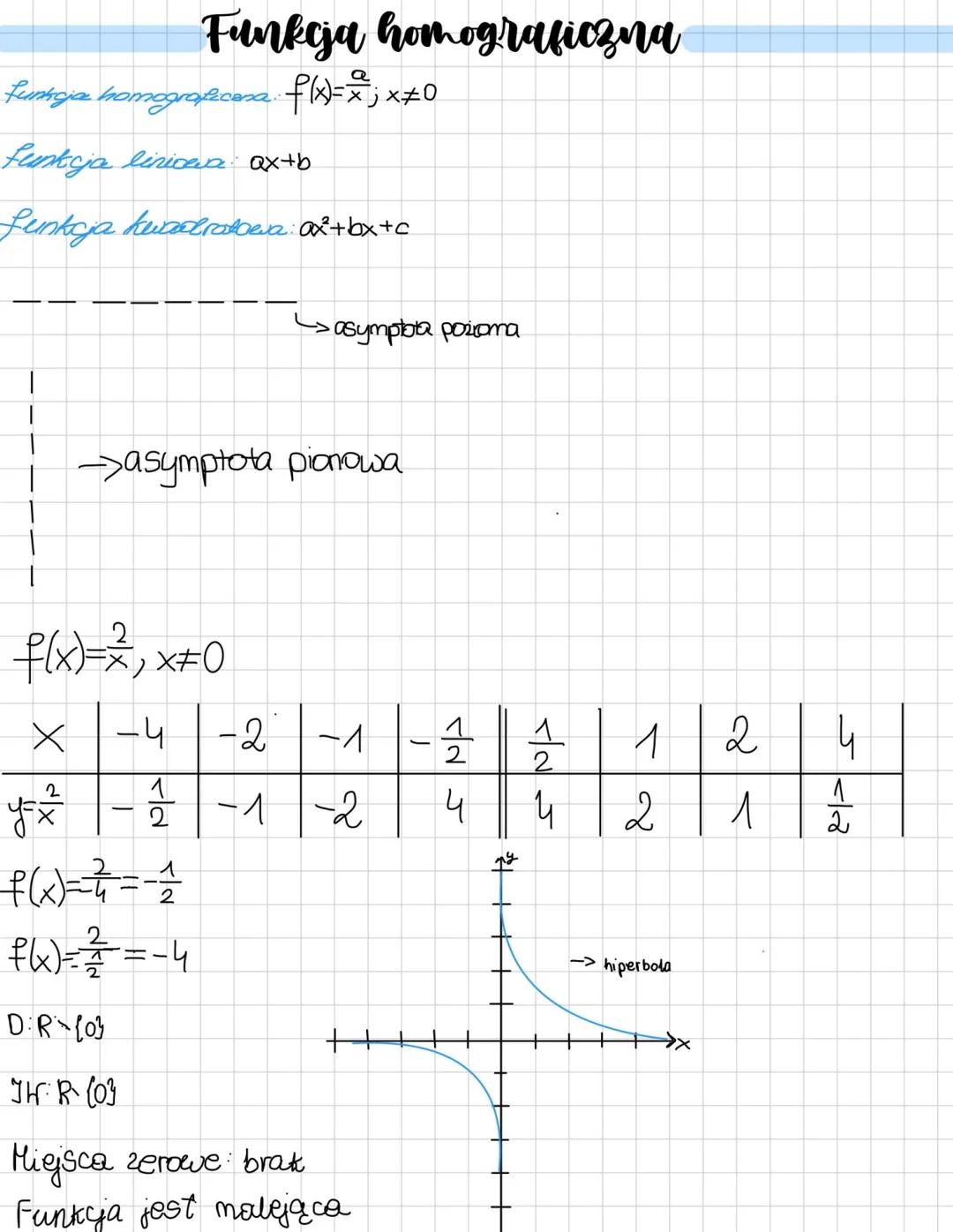
Metodyka: Zawsze rysuj asymptoty jako pierwsze - to szkielet twojego wykresu!

of 6

Wyznaczanie parametrów z wzoru

Najtrудniejsze zadania wymagają wyznaczenia współczynnika a i wektora przesunięcia z danego wzoru funkcji. Kluczowe są przekształcenia algebraiczne.

Dla $f(x) = \frac{3}{x+5}$ od razu widzisz: $a = 3$ i $\vec{u} = [-5, 0]$ . Gorzej z $f(x) = \frac{3x-5}{x-2}$ - musisz wydzielić część całkowitą.

Przekształcasz: $\frac{3x-5}{x-2} = \frac{3(x-2)+1}{x-2} = 3 + \frac{1}{x-2}$ . Teraz widzisz: $a = 1$ , $\vec{u} = [2, 3]$ .

Pro tip: Zawsze wydzielaj część całkowitą przez dzielenie wielomianów - to klucz do sukcesu!

Myśleliśmy, że nigdy nie zapytasz...

Nasz asystent AI jest specjalnie dostosowany do potrzeb uczniów. W oparciu o miliony treści, które mamy na platformie, możemy udzielać uczniom naprawdę znaczących i trafnych odpowiedzi. Ale nie chodzi tylko o odpowiedzi, towarzysz prowadzi również uczniów przez codzienne wyzwania związane z nauką, ze spersonalizowanymi planami nauki, quizami lub treściami na czacie i 100% personalizacją opartą na umiejętnościach i rozwoju uczniów.

Aplikację możesz pobrać z Google Play i Apple Store.

Tak, masz całkowicie darmowy dostęp do wszystkich notatek w aplikacji, możesz w każdej chwili rozmawiać z Ekspertami lub ich obserwować. Możesz użyć punktów, aby odblokować pewne funkcje w aplikacji, które również możesz otrzymać za darmo. Dodatkowo oferujemy usługę Knowunity Premium, która pozwala na odblokowanie większej liczby funkcji.

Podstawowa funkcja homograficzna

Przesuwanie wykresu funkcji

Postać kanoniczna i ogólna definicja

Rozwiązywanie zadań praktycznych

Analiza wykresów i przekształcenia

Wyznaczanie parametrów z wzoru

Myśleliśmy, że nigdy nie zapytasz...

Czym jest Towarzysz AI z Knowunity?

Gdzie mogę pobrać aplikację Knowunity?

Czy aplikacja Knowunity naprawdę jest darmowa?

Podobne notatki

Analiza Funkcji Wymiernej

Właściwości Funkcji Wymiernej

Funkcje Wymierne: Mnożenie i Dzielenie

Funkcje Wymierne i Homograficzne

Wzory Figur Geometrycznych

Obliczanie Przekątnej Kwadratu

Najpopularniejsze notatki: funkcja wymierna

Analiza Funkcji Wymiernej

Funkcje Wymierne i Homograficzne

Funkcje Wymierne: Mnożenie i Dzielenie

Najpopularniejsze notatki z Matematyka

Egzamin ósmoklasisty: Matematyka

Operacje na Pierwiastkach

Mnożenie i dzielenie ułamków

Tabliczka mnożenia od 1 do 100 Klasa 1-4

Ułamki Dziesiętne: Operacje

WYRAŻENIA ALGEBRAICZNE

Trygonometria

Tabliczka Mnożenia 1-100

Wzory Matematyczne na Egzamin

Najpopularniejsze notatki

Zasady Prawo Jazdy B

Analiza Makbeta

Antyk / Starożytność

Lalka

Interakcje Ekologiczne

Andrzej Kmicic: Bohater Potopu

Chemia Organizmu: Kluczowe Składniki

Egzamin ósmoklasisty: Matematyka

Części Mowy w Języku Polskim

Zobacz, co mówią o nas nasi użytkownicy. Pokochali nas — pokochasz też i Ty.

Zarejestruj się, aby zobaczyć notatkę. To nic nie kosztuje!

Podstawowa funkcja homograficzna

Zarejestruj się, aby zobaczyć notatkę. To nic nie kosztuje!

Przesuwanie wykresu funkcji

Zarejestruj się, aby zobaczyć notatkę. To nic nie kosztuje!

Postać kanoniczna i ogólna definicja

Zarejestruj się, aby zobaczyć notatkę. To nic nie kosztuje!

Rozwiązywanie zadań praktycznych

Zarejestruj się, aby zobaczyć notatkę. To nic nie kosztuje!

Analiza wykresów i przekształcenia

Zarejestruj się, aby zobaczyć notatkę. To nic nie kosztuje!

Wyznaczanie parametrów z wzoru

Myśleliśmy, że nigdy nie zapytasz...

Czym jest Towarzysz AI z Knowunity?

Gdzie mogę pobrać aplikację Knowunity?

Czy aplikacja Knowunity naprawdę jest darmowa?

Podobne notatki

Analiza Funkcji Wymiernej

Właściwości Funkcji Wymiernej

Funkcje Wymierne: Mnożenie i Dzielenie

Funkcje Wymierne i Homograficzne

Wzory Figur Geometrycznych

Obliczanie Przekątnej Kwadratu

Najpopularniejsze notatki: funkcja wymierna

Analiza Funkcji Wymiernej

Funkcje Wymierne i Homograficzne

Funkcje Wymierne: Mnożenie i Dzielenie

Najpopularniejsze notatki z Matematyka

Egzamin ósmoklasisty: Matematyka

Operacje na Pierwiastkach

Mnożenie i dzielenie ułamków

Tabliczka mnożenia od 1 do 100 Klasa 1-4

Ułamki Dziesiętne: Operacje

WYRAŻENIA ALGEBRAICZNE

Trygonometria

Tabliczka Mnożenia 1-100

Wzory Matematyczne na Egzamin

Najpopularniejsze notatki