Funkcja wykładnicza

Funkcja wykładnicza to funkcja postaci f(x) = a^x, gdzie a > 0 i a ≠ 1. Jej właściwości zależą od wartości podstawy a.

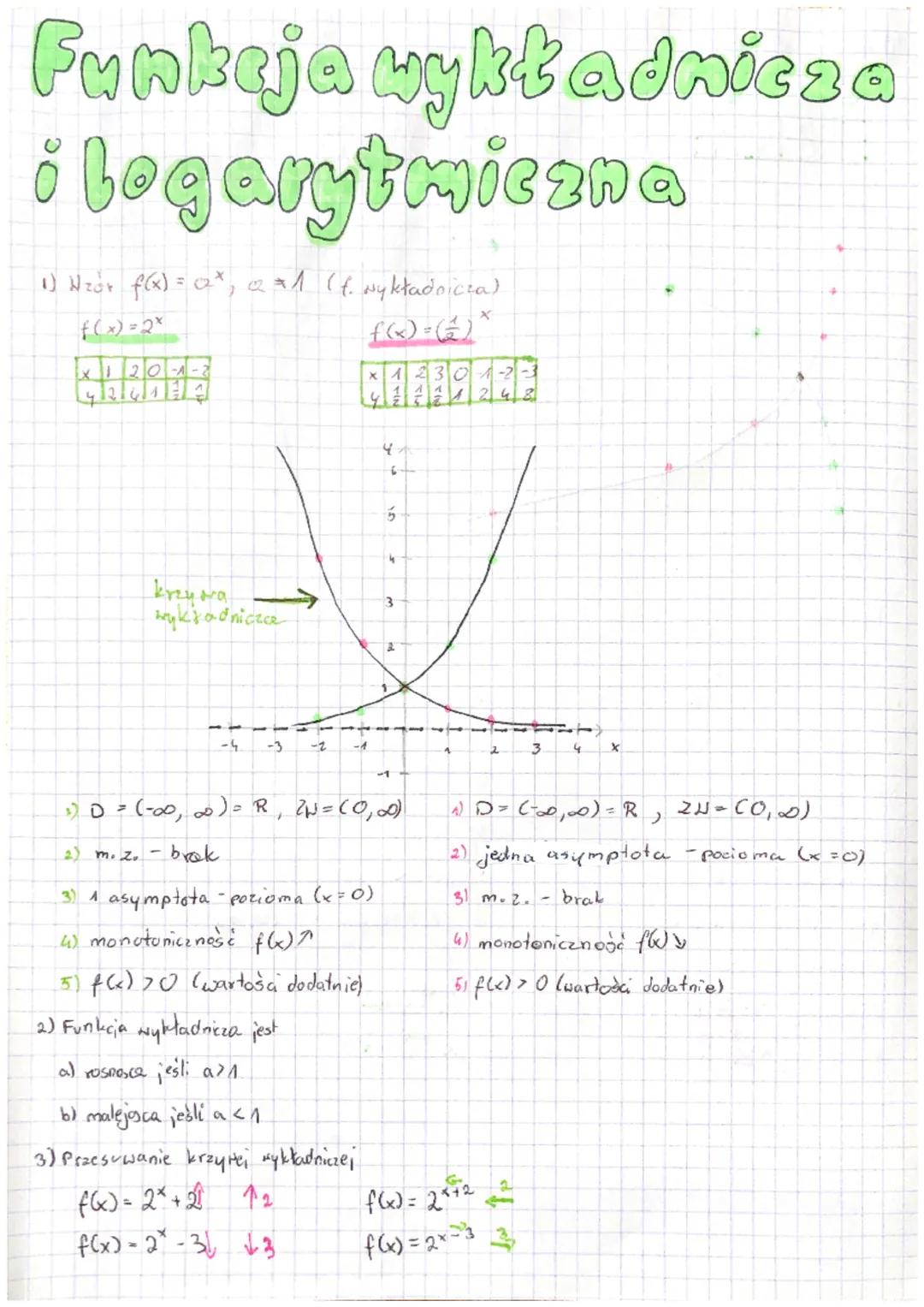
Dla funkcji rosnącej (a > 1), np. f(x) = 2^x, wartości rosną coraz szybciej dla x > 0 i zbliżają się do zera dla x < 0. Z kolei dla funkcji malejącej (0 < a < 1), np. f(x) = (1/2)^x, wartości maleją dla x > 0 i rosną dla x < 0.

Ważne właściwości funkcji wykładniczej:

• Dziedzina to wszystkie liczby rzeczywiste: D = R
• Zbiór wartości to tylko liczby dodatnie: ZW = (0, ∞)
• Posiada asymptotę poziomą (oś x)
• Nie posiada miejsc zerowych
• Zawsze przyjmuje wartości dodatnie

💡 Warto zapamiętać: Funkcja wykładnicza przechodzi zawsze przez punkt (0,1), niezależnie od wartości podstawy a. To dlatego, że a^0 = 1 dla każdej niezerowej podstawy.

Możemy przesuwać wykres funkcji wykładniczej:

• Poziomo: f(x) = a^$x+c$ przesuwa wykres o c jednostek w lewo
• Poziomo: f(x) = a^$x-c$ przesuwa wykres o c jednostek w prawo

Funkcja logarytmiczna

Funkcja logarytmiczna f(x) = log_a(x) jest funkcją odwrotną do funkcji wykładniczej. Jej wykres znajduje się wyłącznie w I i IV ćwiartce układu współrzędnych.

Kluczowe właściwości funkcji logarytmicznej:

• Dziedzina to tylko liczby dodatnie: D = (0, ∞)
• Zbiór wartości to wszystkie liczby rzeczywiste: ZW = R
• Posiada jedną asymptotę pionową $oś y, czyli x = 0$
• Ma dokładnie jedno miejsce zerowe: x = 1 $bo log_a(1) = 0$

W zależności od przedziału argumentu, funkcja logarytmiczna przyjmuje różne znaki. Dla podstawy a > 1: funkcja przyjmuje wartości ujemne gdy x ∈ (0,1) oraz dodatnie gdy x ∈ (1,∞).

💡 Wskazówka praktyczna: Wykres funkcji logarytmicznej można łatwo naszkicować, jeśli pamiętasz, że jest on odbiciem wykresu odpowiedniej funkcji wykładniczej względem prostej y = x.

Podobnie jak funkcję wykładniczą, możemy przesuwać wykres funkcji logarytmicznej:

• W poziomie: f(x) = log_a$x-c$ przesuwa wykres o c jednostek w prawo
• W poziomie: f(x) = log_a$x+c$ przesuwa wykres o c jednostek w lewo