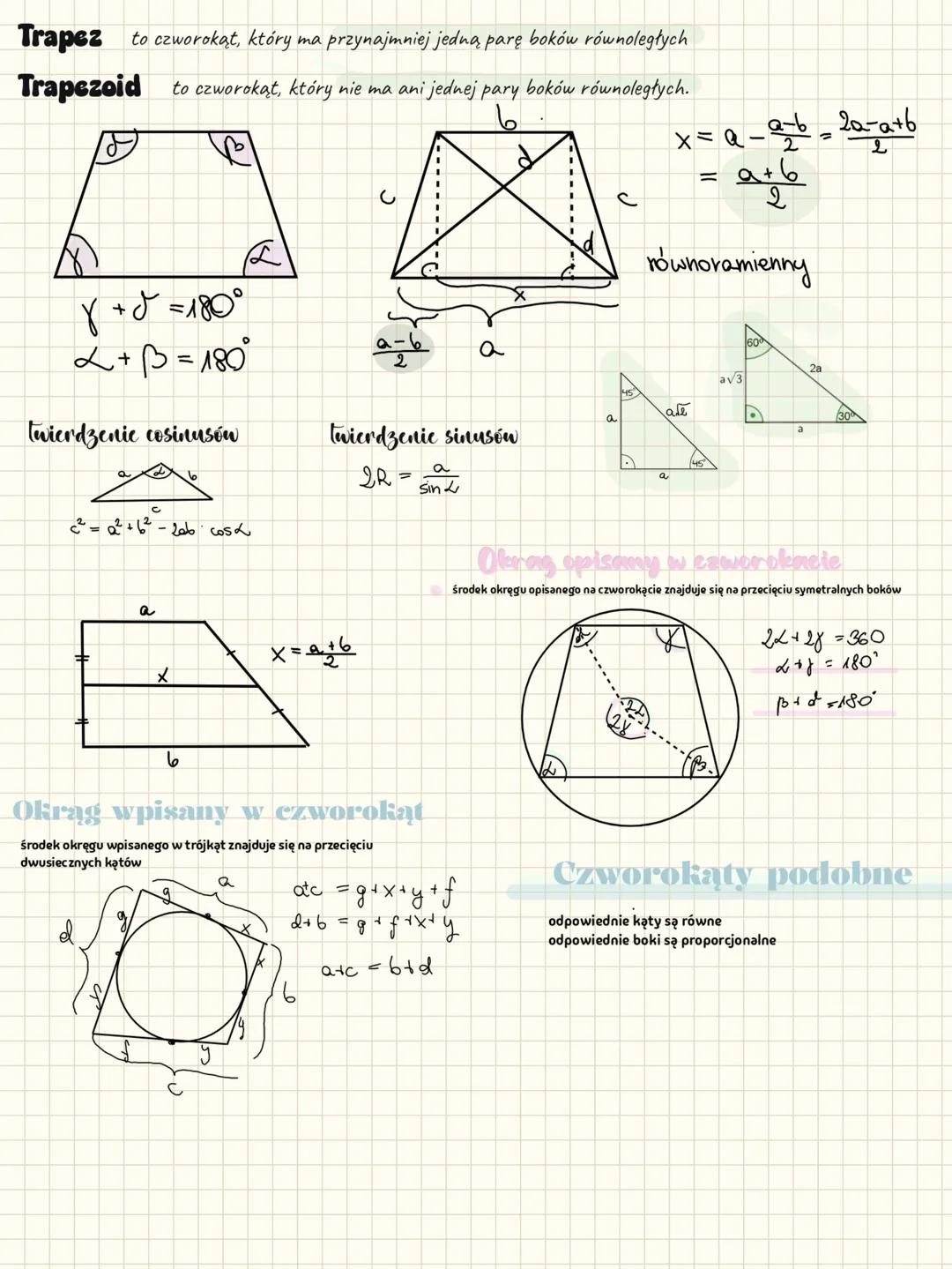
Pola figur płaskich
Znając odpowiednie wzory, obliczenie pola dowolnej figury płaskiej staje się proste. Dla trójkąta masz kilka możliwości: P = (1/2)ab·sinγ, P = abc/(4R), gdzie R to promień okręgu opisanego, lub P = p·r, gdzie p to połowa obwodu, a r to promień okręgu wpisanego.
Jednym z najpotężniejszych narzędzi jest wzór Herona: P = √p(p−a)(p−b)(p−c), gdzie p = a+b+c/2. Pozwala on obliczyć pole trójkąta znając tylko długości jego boków.
Dla czworokątów wzory są równie przydatne. Prostokąt: P = a·b; kwadrat: P = a² lub P = (1/2)d² (gdzie d to przekątna); równoległobok: P = a·ha lub P = a·b·sinγ; romb: P = a·ha, P = a²·sinγ lub P = (1/2)·d₁·d₂ (gdzie d₁ i d₂ to przekątne).
Wskazówka praktyczna! Pole trapezu obliczysz ze wzoru P = (a+b)/2·h, gdzie a i b to długości podstaw, a h to wysokość. To jak obliczenie średniej z podstaw i pomnożenie jej przez wysokość.
Mając te wzory w pamięci, łatwo rozwiążesz większość zadań związanych z polami czworokątów i trójkątów na klasówkach.