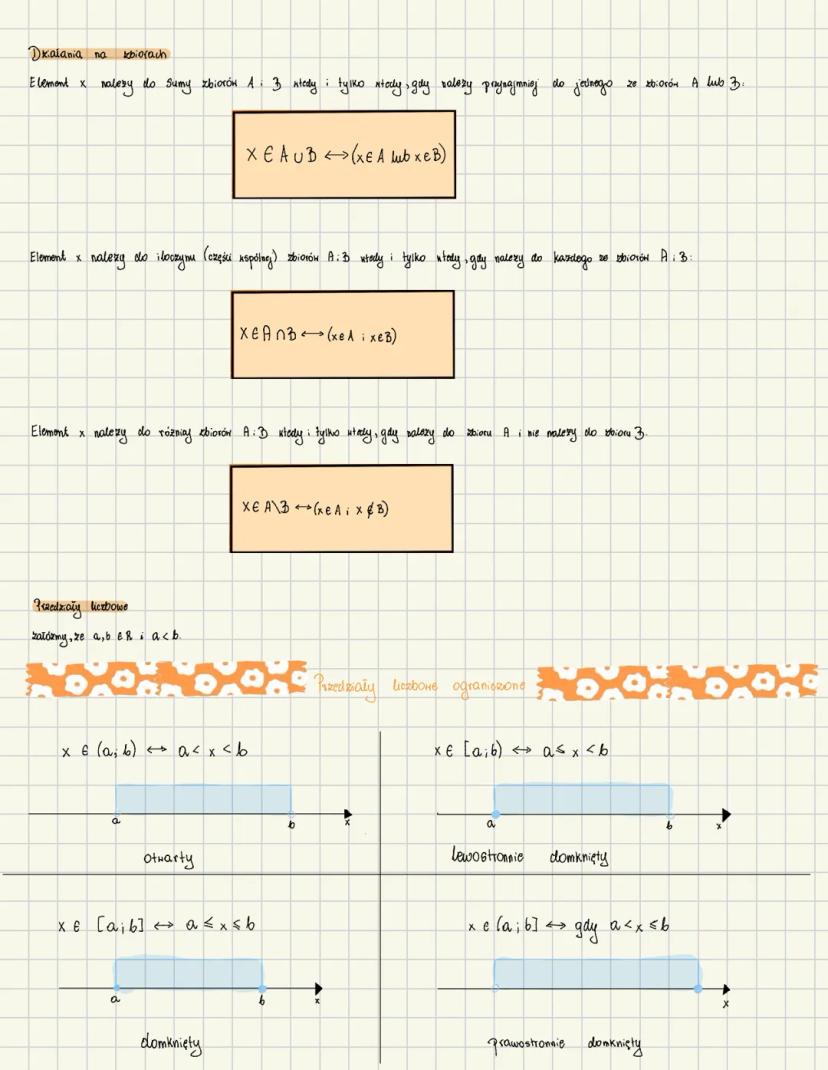
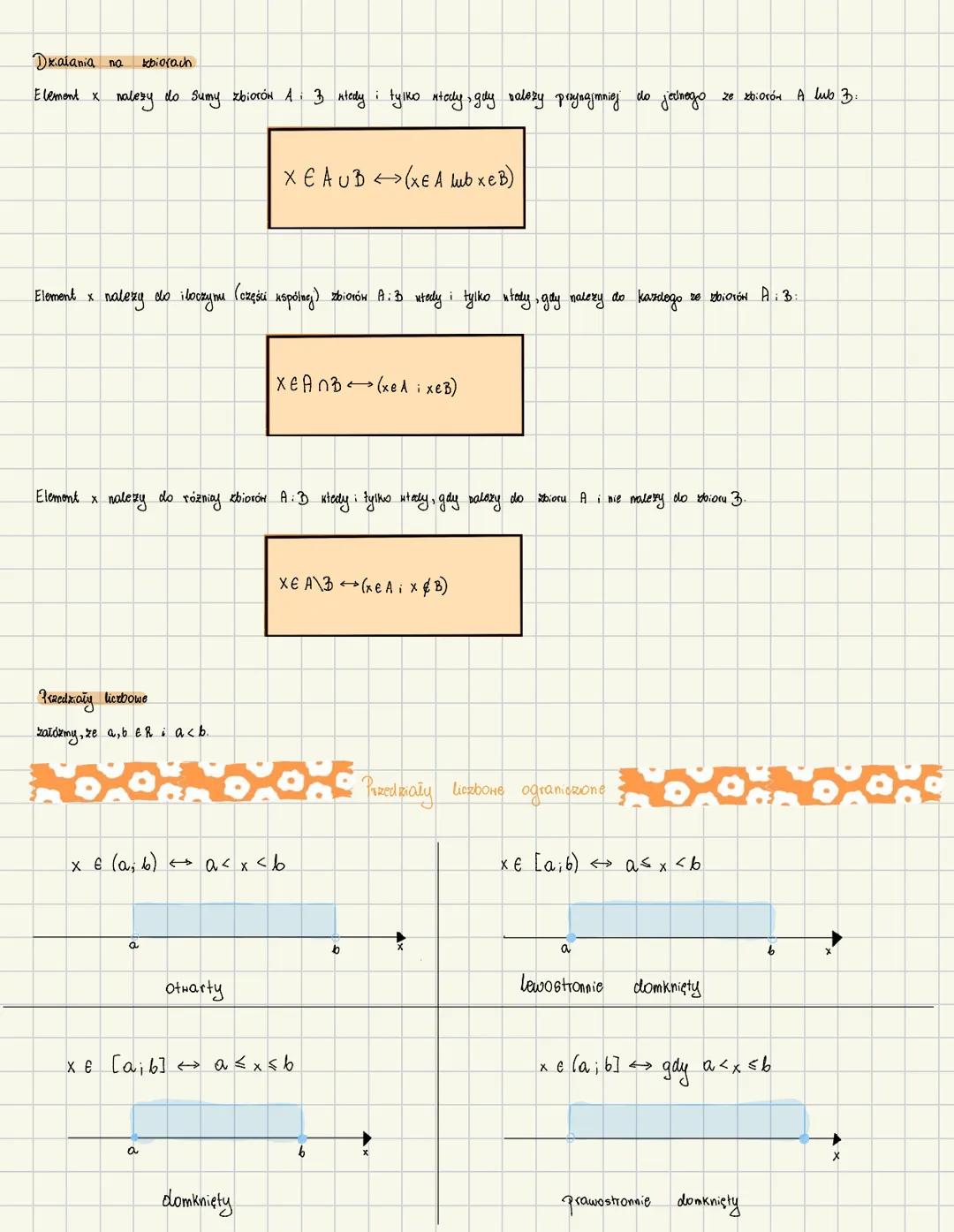
Liczby rzeczywiste i wyrażenia algebraiczne

Ten dział matematyki stanowi podstawę dalszej edukacji matematycznej. Będziesz pracować z różnymi rodzajami liczb - od naturalnych przez wymierne aż po niewymierne.

Zrozumienie struktury zbiorów liczbowych pomoże Ci rozwiązywać złożone problemy matematyczne w przyszłości. Od tego zaczyna się cała algebra!

Wskazówka: Pamiętaj, że wszystkie poznane wcześniej typy liczb są częścią większego zbioru - liczb rzeczywistych. To podstawa dla zrozumienia kolejnych tematów.

Liczby rzeczywiste i ich właściwości

Liczby rzeczywiste (R) możemy podzielić na kilka istotnych podzbiorów. Liczby naturalne (N) to {0, 1, 2, 3, ...}, a liczby całkowite (Z) to {..., -3, -2, -1, 0, 1, 2, 3, ...}.

Liczby wymierne (Q) to wszystkie liczby, które można zapisać jako ułamek p/q, gdzie p i q są liczbami całkowitymi, a q ≠ 0. Mają one rozwinięcie dziesiętne skończone lub nieskończone okresowe (np. 0,125 lub 0,111...). Z kolei liczby niewymierne $R\Q$ mają rozwinięcie dziesiętne nieskończone i nieokresowe $np. π = 3,141592...$.

W zbiorze liczb naturalnych ważne jest pojęcie podzielności. Dla każdej pary liczb w i d istnieje dokładnie jedna para liczb n i r, że w = n·d + r i r < d. Jeśli r = 0, mówimy, że w jest podzielne przez d. Liczba pierwsza to liczba większa od 1, której jedynymi dzielnikami są 1 i ona sama.

Uwaga! Liczby 0 i 1 nie są ani pierwsze, ani złożone. Liczba 2 jest jedyną parzystą liczbą pierwszą.

Działania na zbiorach i przedziały liczbowe

Działania na zbiorach to podstawa matematyki. Suma zbiorów (A∪B) zawiera wszystkie elementy należące do przynajmniej jednego ze zbiorów. Iloczyn zbiorów (A∩B) zawiera tylko elementy wspólne dla obu zbiorów.

Różnica zbiorów $A\B$ to wszystkie elementy, które należą do A, ale nie należą do B. Te operacje pozwalają nam precyzyjnie opisywać relacje między zbiorami.

Przedziały liczbowe to sposób opisywania fragmentów osi liczbowej. Dla liczb a, b ∈ R, gdzie a < b, rozróżniamy różne typy przedziałów: otwarte (a,b), domknięte [a,b] oraz przedziały półotwarte [a,b) i (a,b]. Przedziały mogą być również nieograniczone, np. (−∞,a) lub [a,∞).

Pro-tip: Przy rozwiązywaniu zadań z działaniami na zbiorach narysuj diagram Venna - to świetna metoda wizualizacji i pomoże Ci uniknąć błędów!

Przedziały nieograniczone i zadania praktyczne

Przedziały nieograniczone opisują liczby większe lub mniejsze od danej wartości. Gdy piszemy x ∈ (−∞,a), oznacza to wszystkie x mniejsze od a. Podobnie x ∈ (a,∞) to wszystkie x większe od a.

W matematyce istotna jest umiejętność dowodzenia twierdzeń. Na przykład, możemy pokazać, że dla liczby pierwszej p, wyrażenie p²−p+2 nie jest liczbą pierwszą. Wystarczy zauważyć, że p²−p+2 = p(p−1)+2, gdzie iloczyn p(p−1) jest zawsze parzysty (bo jedna z liczb musi być parzysta).

Podobnie możemy udowodnić, że dla dowolnej liczby naturalnej k wyrażenie k²+k+17 jest liczbą nieparzystą. Wystarczy zapisać k$k+1$+17 i zauważyć, że k$k+1$ jest zawsze liczbą parzystą.

Zapamiętaj: Podczas dowodzenia szukaj wzorów i prawidłowości - często przekształcenie wyrażenia na inną, równoważną postać znacznie ułatwia rozwiązanie!

Podzielność i dowodzenie twierdzeń

Dowodzenie twierdzeń dotyczących podzielności to ważna umiejętność matematyczna. Spójrz, jak możemy udowodnić, że iloczyn kwadratów trzech kolejnych liczb naturalnych jest podzielny przez 36.

Niech n-1, n, n+1 będą trzema kolejnymi liczbami naturalnymi. Iloczyn ich kwadratów możemy zapisać jako: $n-1$²·n²·$n+1$² = $(n-1)·n·(n+1)$².

Przekształcając dalej: $(n-1)·n·(n+1)$² = $n³-n$² = $n(n²-1)$² = $n(n-1)(n+1)$².

Kluczowe obserwacje: wśród trzech kolejnych liczb naturalnych zawsze jedna jest podzielna przez 3, a przynajmniej jedna przez 2. Zatem ich iloczyn jest podzielny przez 6, a kwadrat tego iloczynu przez 36.

Wskazówka praktyczna: Przy dowodzeniu twierdzeń o podzielności szukaj prawidłowości związanych z liczbami podzielnymi przez 2 i 3 - to najczęstsze przypadki!