Praktyczne zastosowanie wzorów Cramera
Pora na konkretny przykład! Masz układ trzech równań z trzema niewiadomymi - teraz pokażę ci, jak to rozłożyć na czynniki pierwsze.
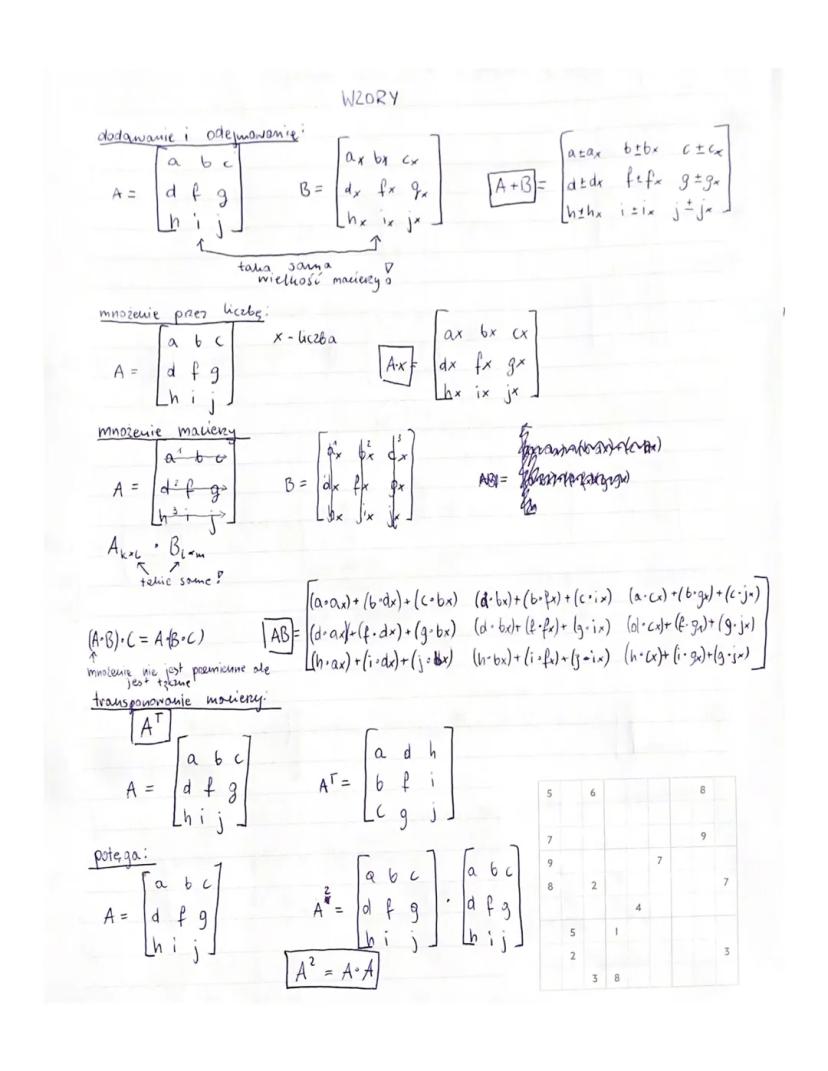
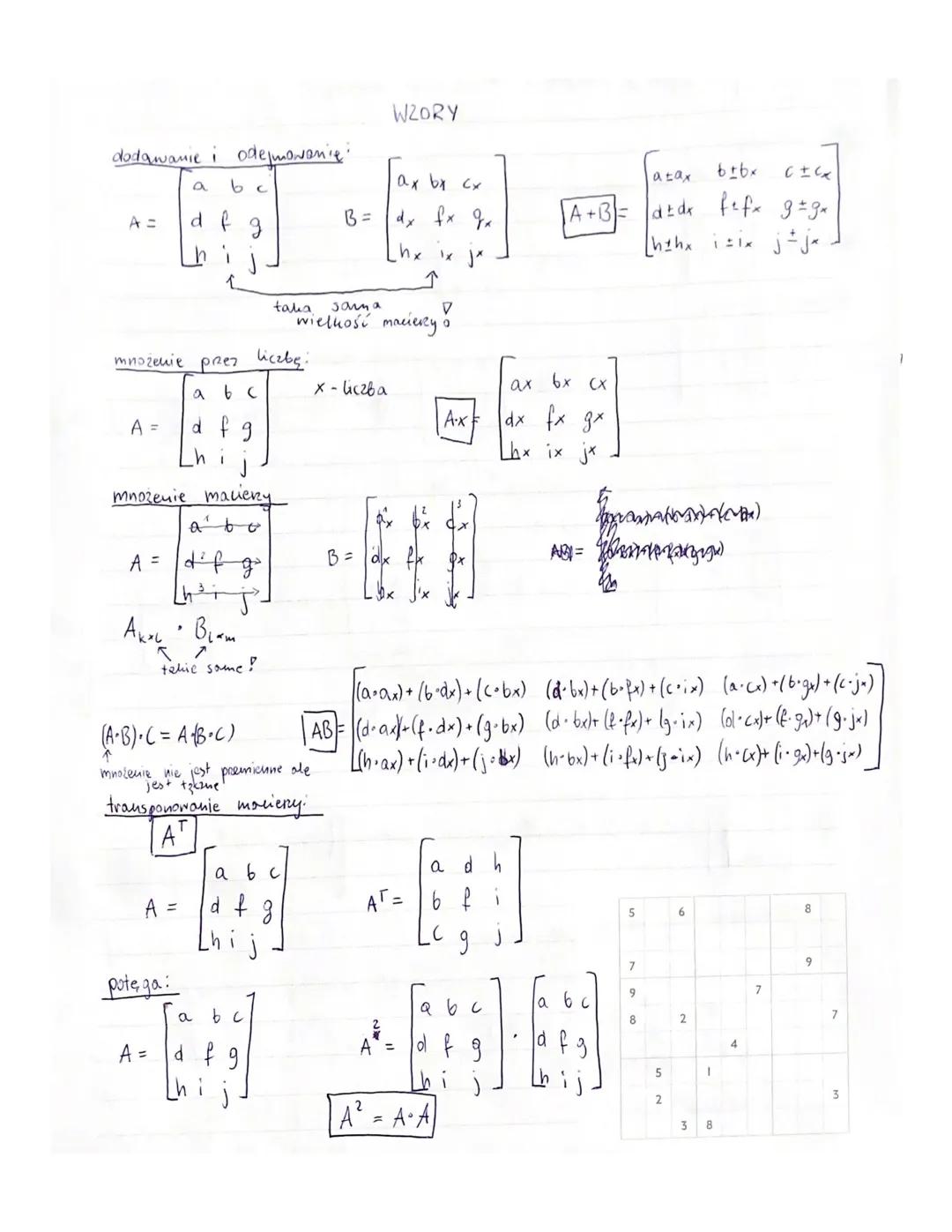
Najpierw wydzielasz macierze: A (współczynniki przy niewiadomych), B (wyrazy wolne), X (niewiadome). To jak segregowanie śmieci - każda rzecz ma swoje miejsce.
Kolejność działania jest zawsze taka sama: 1) Oblicz det A, 2) Oblicz det A₁, det A₂, det A₃ (podstawiając wektor B), 3) Podziel i otrzymaj x₁, x₂, x₃.
💡 Pro tip: Jeśli det A = 0, układ albo nie ma rozwiązań, albo ma nieskończenie wiele rozwiązań.
Pamiętaj, że kolejność ma znaczenie - pierwsza kolumna zamieniana dla x₁, druga dla x₂, trzecia dla x₃. Jeden błąd w kolejności i cały wynik pójdzie w błoto!