Matematyka

Twierdzenia o przystawaniu i podobieństwie trójkątów

Twierdzenie Pitagorasa

248

•

Zaktualizowano Mar 24, 2026

•

3 strony

Twierdzenie Pitagorasa – Przykładowe Zadanie dla Klasy 8

Arek Flo

@arekflo

Sprawdź, jak rozwiązać zadania z twierdzenia Pitagorasa! Oto prosty przewodnik,... Pokaż więcej

1 / 3

$# MATEMATYKA $a²+b²=c²$ zad 1 24 18 $a² + b² = c²$ x=30 $24² + 18² = x²$ $576 + 324 = x²$ $x = \sqrt{900}=30$ Odp: Równa się 30cm$

Twierdzenie Pitagorasa w praktyce

Twierdzenie Pitagorasa mówi, że w trójkącie prostokątnym suma kwadratów przyprostokątnych równa się kwadratowi przeciwprostokątnej: a² + b² = c². To podstawowe narzędzie do rozwiązywania wielu zadań geometrycznych.

W pierwszym przykładzie mamy: 16² + x² = 34². Rozwiązując równanie: 256 + x² = 1156, więc x² = 900, a x = 30 cm. W drugim zadaniu szukamy przeciwprostokątnej, gdy znamy przyprostokątne: 24² + 18² = x², czyli 576 + 324 = x², co daje x = 30.

Pamiętaj, że wzór P = a·h/2 pozwala obliczyć pole trójkąta, jeśli znasz podstawę i wysokość. Przyda Ci się to przy bardziej złożonych zadaniach z twierdzeniem Pitagorasa.

💡 Wskazówka: Zawsze sprawdzaj jednostki w odpowiedzi! Jeśli dane są w centymetrach, wynik również powinien być w centymetrach.

$# MATEMATYKA $a²+b²=c²$ zad 1 24 18 $a² + b² = c²$ x=30 $24² + 18² = x²$ $576 + 324 = x²$ $x = \sqrt{900}=30$ Odp: Równa się 30cm$

Rozwiązywanie równań z twierdzeniem Pitagorasa

Twierdzenie Pitagorasa pomaga też rozwiązywać zadania z niewiadomymi. Na przykład, gdy jedna z przyprostokątnych jest wyrażona wzorem, jak w zadaniu: (2x)² + x² = 5². Rozwijając: 4x² + x² = 25, czyli 5x² = 25, co daje x = √5 ≈ 2,24.

Przy obliczaniu obwodu figury zawierającej trójkąt prostokątny, najpierw znajdź brakujące boki. W zadaniu z obwodem 65 cm², musisz użyć twierdzenia Pitagorasa do znalezienia długości wszystkich boków przed sumowaniem.

W bardziej złożonym przykładzie: 8² + x² = 14², czyli 64 + x² = 196, co daje x² = 132, a x = √132 ≈ 11,5 cm. Obliczenia możesz uprościć, rozkładając liczby pod pierwiastkiem.

💡 Pamiętaj: Wartość pierwiastka kwadratowego zawsze możesz sprawdzić, podnosząc wynik do kwadratu – powinien dać liczbę pod pierwiastkiem!

$# MATEMATYKA $a²+b²=c²$ zad 1 24 18 $a² + b² = c²$ x=30 $24² + 18² = x²$ $576 + 324 = x²$ $x = \sqrt{900}=30$ Odp: Równa się 30cm$

Twierdzenie Pitagorasa w obliczeniach pola i obwodu

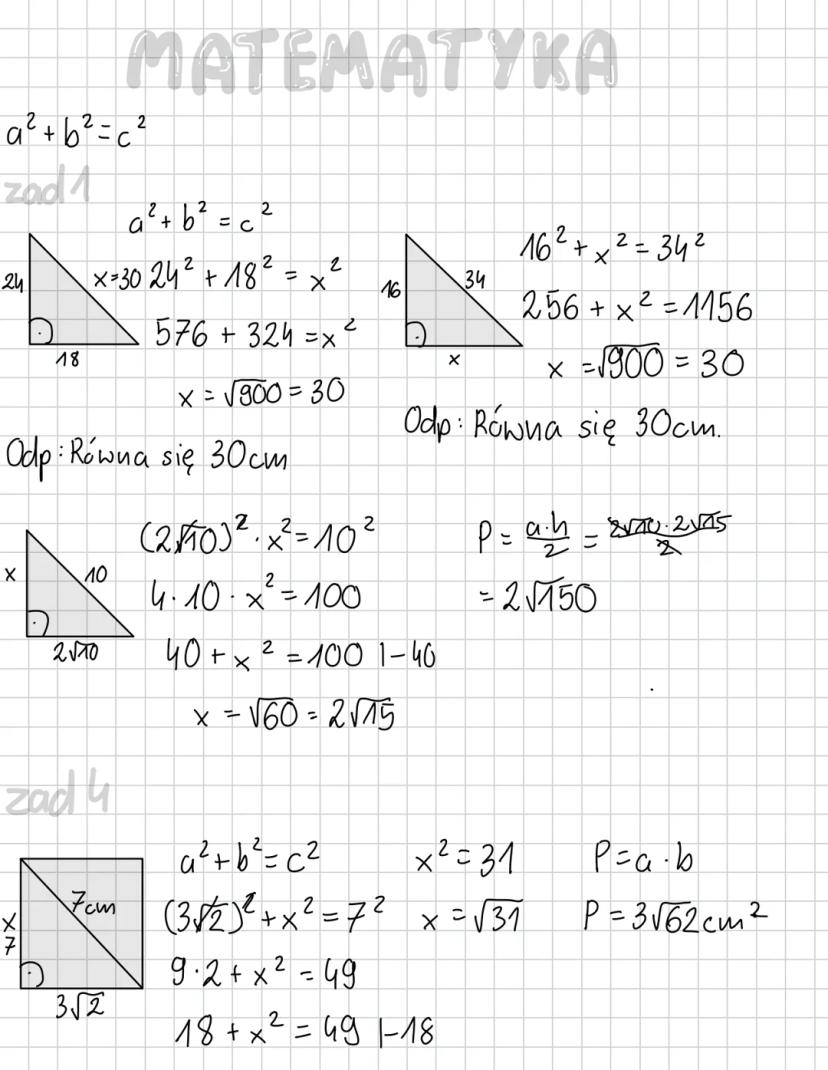
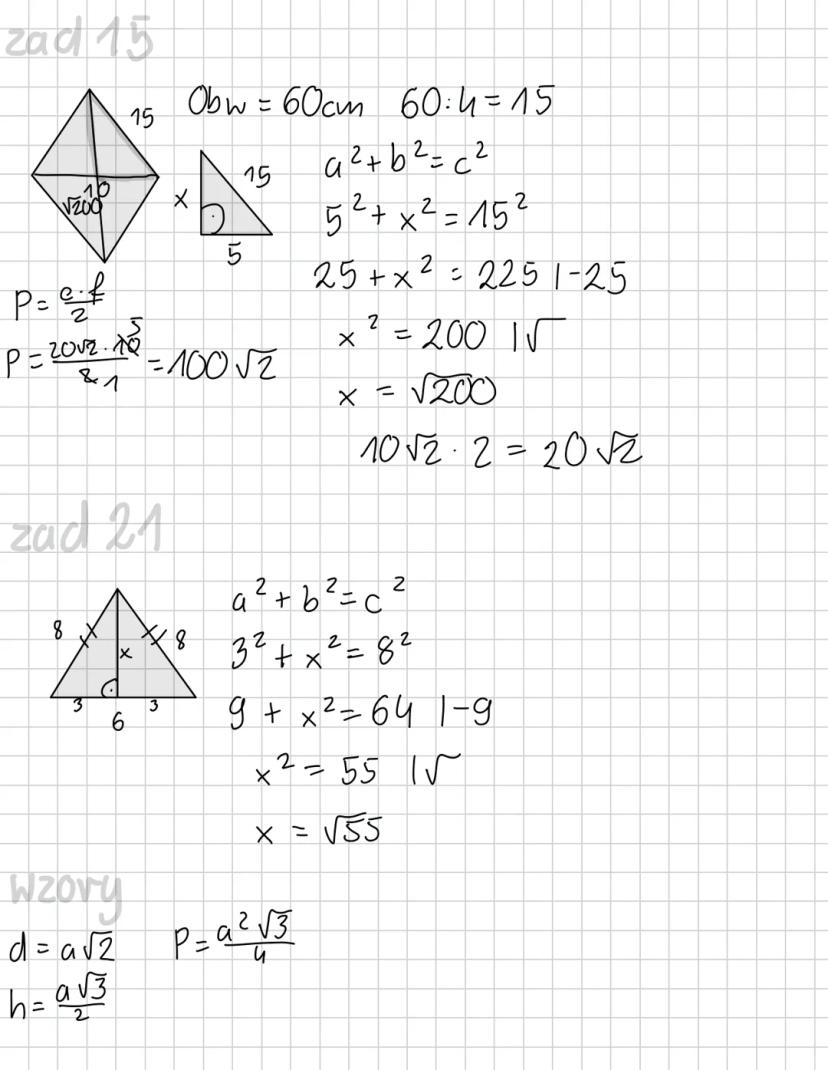
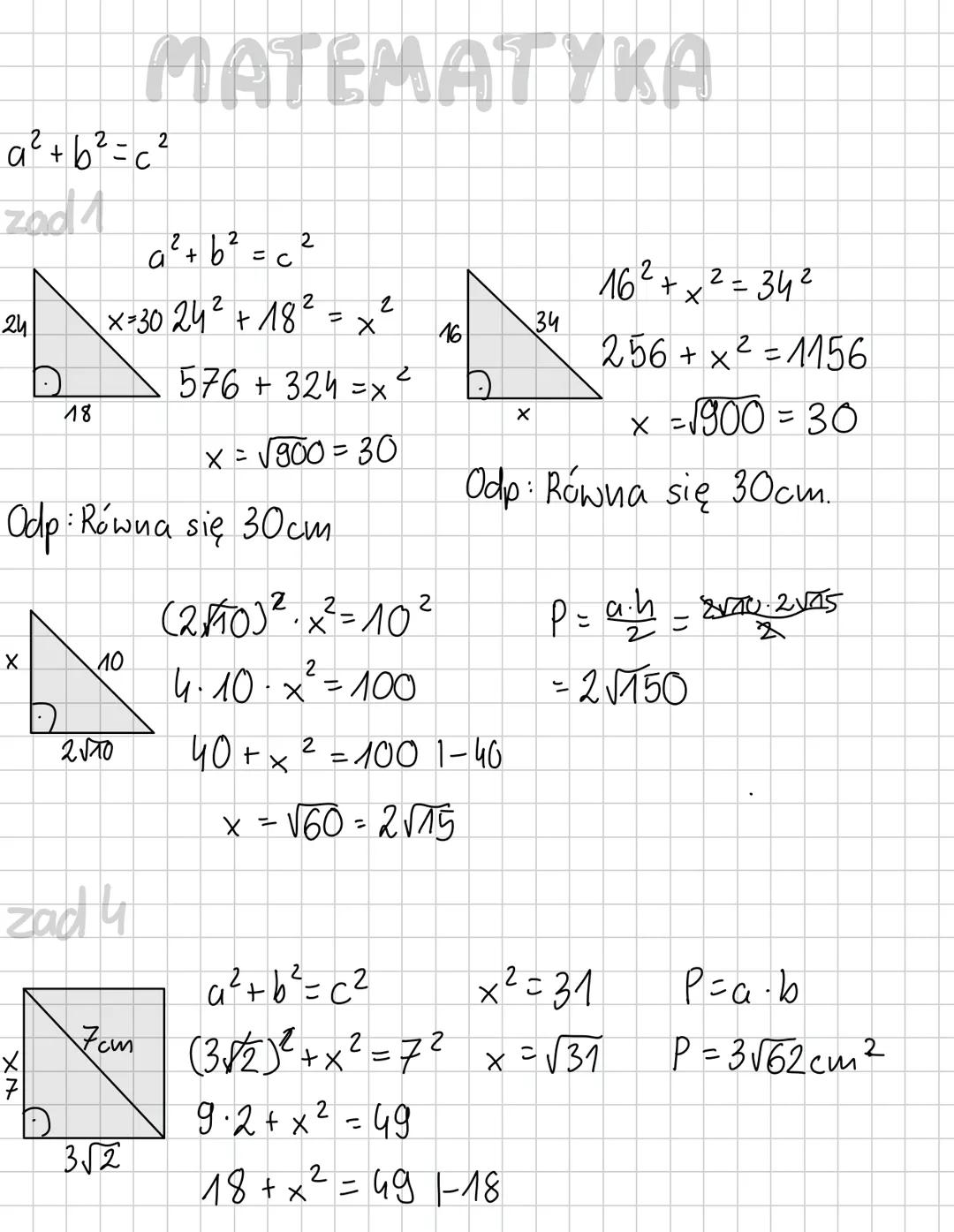
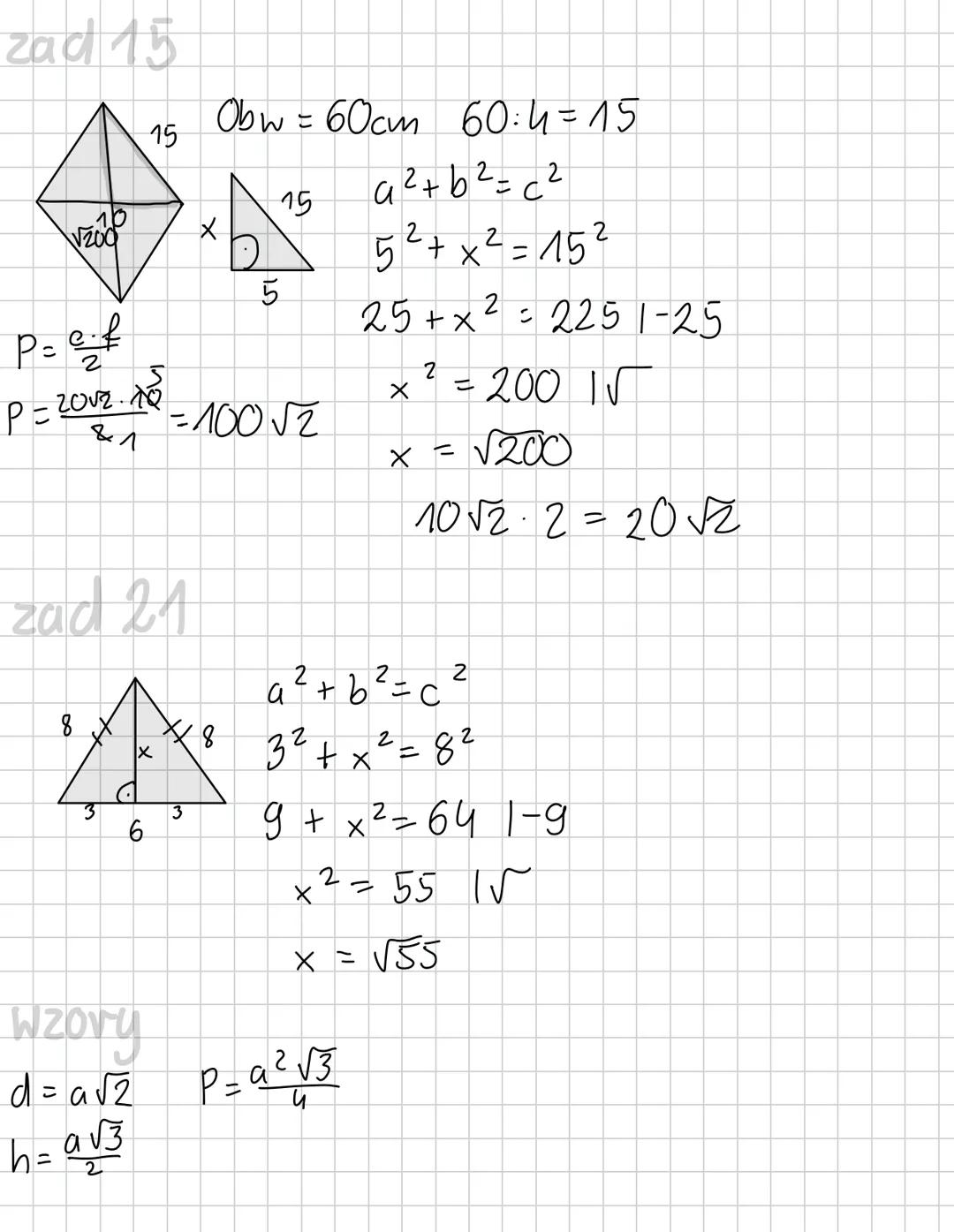
Gdy znasz obwód trójkąta prostokątnego, możesz wyznaczyć jego boki. W zadaniu z obwodem 60 cm, dzieląc przez 4, otrzymujemy 15 cm. Następnie używamy twierdzenia Pitagorasa: 5² + x² = 15², co daje x² = 200, a x = √200 ≈ 14,14.

Pole trójkąta możesz obliczyć, znając jego boki, za pomocą wzoru P = (a·b)/2. Kiedy masz pole równe 100², możesz znaleźć potrzebne wymiary, rozwiązując odpowiednie równanie.

W ostatnim przykładzie mamy: 3² + x² = 8², czyli 9 + x² = 64, co daje x = √55 ≈ 7,42. Twierdzenie Pitagorasa świetnie sprawdza się w zadaniach praktycznych, gdzie szukasz odległości, wysokości czy przekątnych.

💡 Ważne: Wzory na pole $P = a·h/2$ i przekątną $d = a√2$ to niezbędne narzędzia, które często współpracują z twierdzeniem Pitagorasa!

Myśleliśmy, że nigdy nie zapytasz...

Czym jest Towarzysz AI z Knowunity?

Nasz asystent AI jest specjalnie dostosowany do potrzeb uczniów. W oparciu o miliony treści, które mamy na platformie, możemy udzielać uczniom naprawdę znaczących i trafnych odpowiedzi. Ale nie chodzi tylko o odpowiedzi, towarzysz prowadzi również uczniów przez codzienne wyzwania związane z nauką, ze spersonalizowanymi planami nauki, quizami lub treściami na czacie i 100% personalizacją opartą na umiejętnościach i rozwoju uczniów.

Gdzie mogę pobrać aplikację Knowunity?

Aplikację możesz pobrać z Google Play i Apple Store.

Czy aplikacja Knowunity naprawdę jest darmowa?

Tak, masz całkowicie darmowy dostęp do wszystkich notatek w aplikacji, możesz w każdej chwili rozmawiać z Ekspertami lub ich obserwować. Możesz użyć punktów, aby odblokować pewne funkcje w aplikacji, które również możesz otrzymać za darmo. Dodatkowo oferujemy usługę Knowunity Premium, która pozwala na odblokowanie większej liczby funkcji.

Podobne notatki