Analiza wykresu funkcji

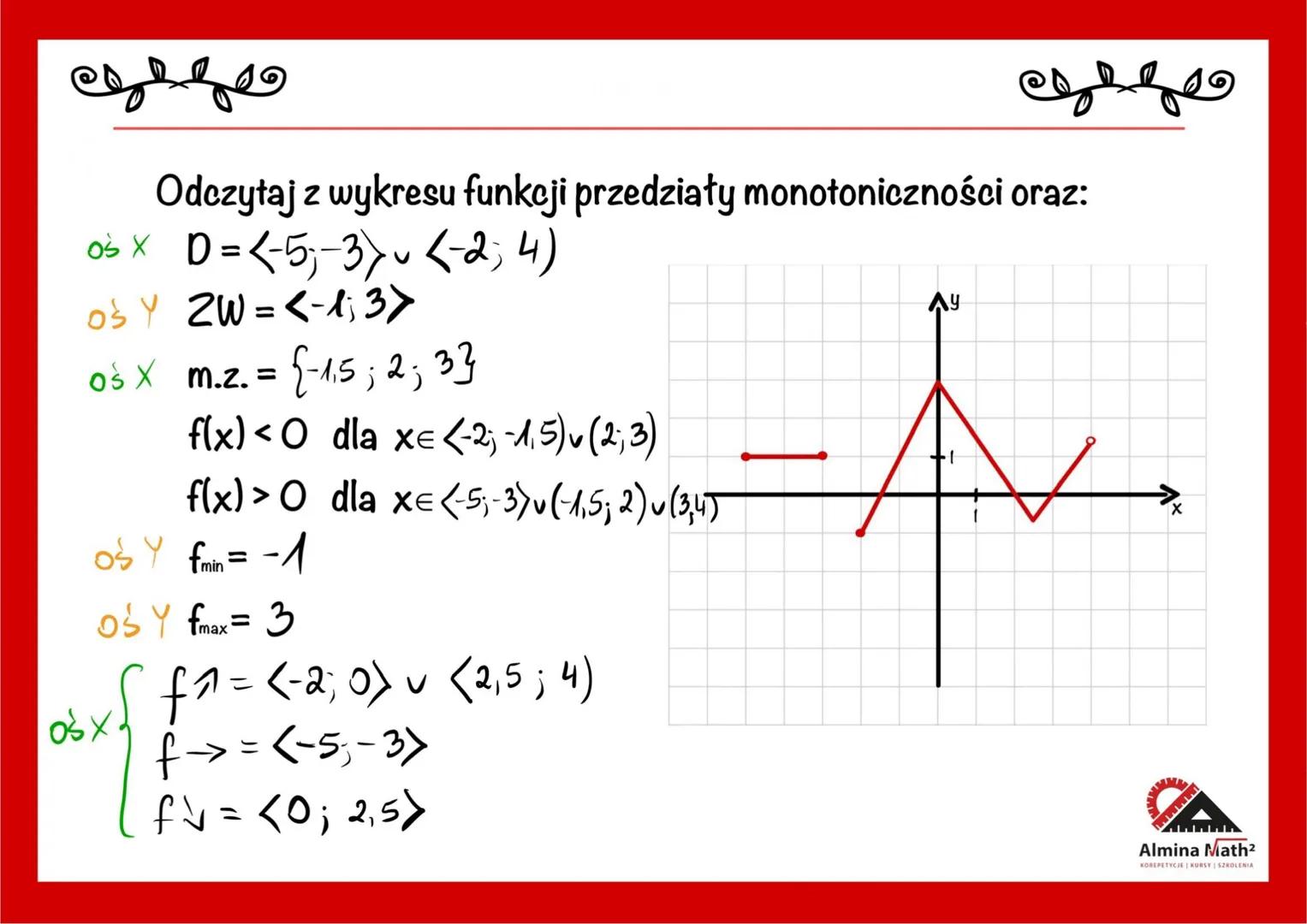
Patrząc na wykres funkcji, możemy odczytać wiele ważnych informacji. Dziedziną tej funkcji jest $D = <-5; -3> \cup <-2; 4)$, czyli funkcja jest określona dla argumentów z tych przedziałów.

Miejsca zerowe funkcji to punkty, w których wykres przecina oś X. W naszym przypadku to wartości $x = -1,5; 2; 3$. Funkcja przyjmuje wartości ujemne dla $x \in <-2; -1,5) \cup (2; 3)$, a dodatnie dla $x \in (-5; -3) \cup (-1,5; 2) \cup (3; 4)$.

Funkcja ma swoje minimum lokalne wynoszące -1 oraz maksimum lokalne równe 3. Jej zbiór wartości to przedział $ZW = <-1; 3>$, co oznacza, że funkcja nigdy nie przyjmuje wartości mniejszych niż -1 ani większych niż 3.

💡 Wskazówka: Monotoniczność funkcji mówi nam, gdzie funkcja rośnie, a gdzie maleje. Ta funkcja jest rosnąca w przedziałach $<-2; 0> \cup <2,5; 4)$, malejąca w przedziale $<-5; -3>$, a stała w przedziale $<0; 2,5>$.