Potęga o wykładniku całkowitym i wymiernym
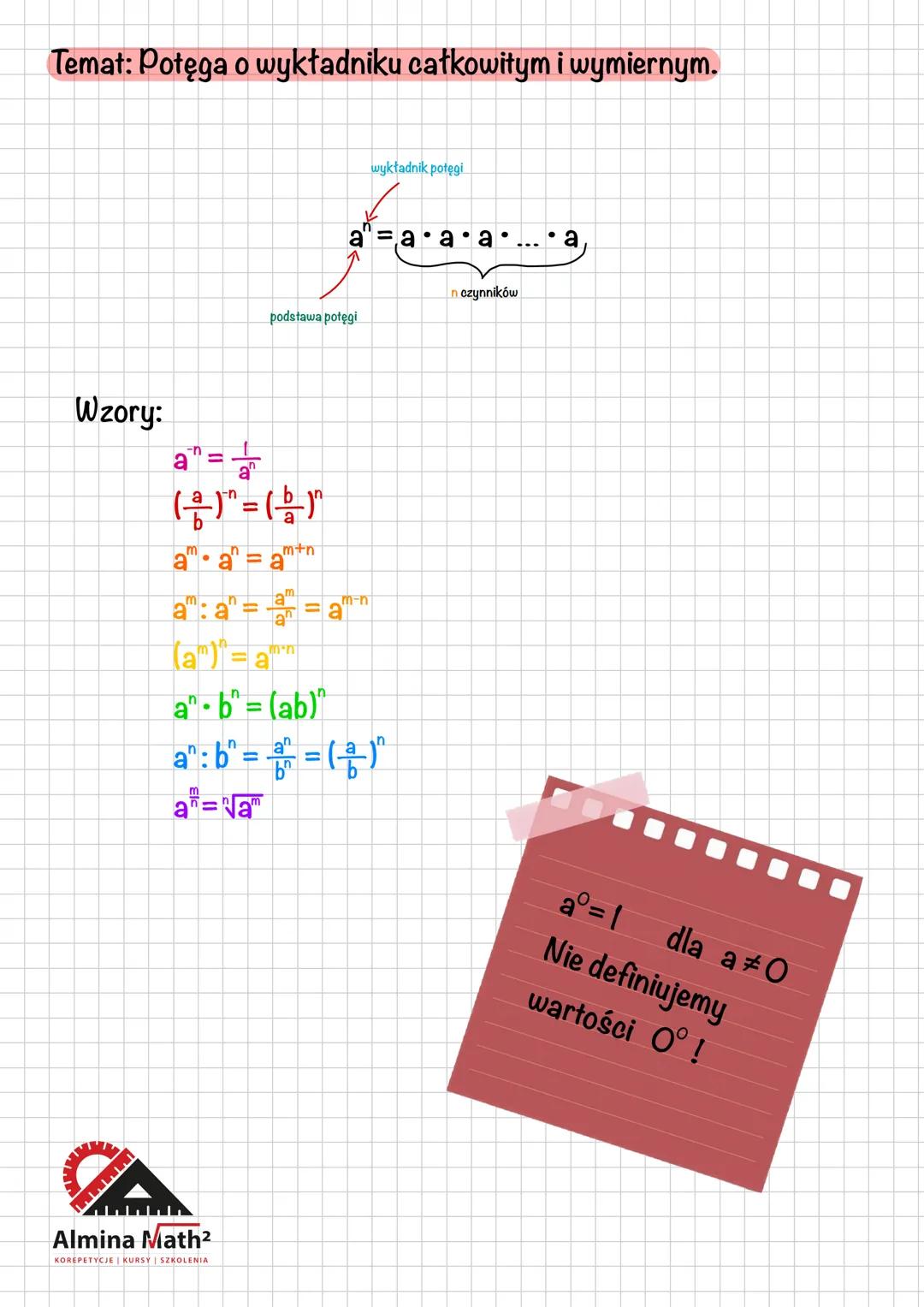
Potęga składa się z dwóch elementów: podstawy (liczba a) oraz wykładnika (liczba n). Gdy zapisujemy aⁿ, oznacza to, że mnożymy liczbę a przez samą siebie n razy. Przykładowo 2³ = 2 · 2 · 2 = 8.
Korzystając z potęg, warto zapamiętać kilka ważnych wzorów. Przy mnożeniu potęg o tej samej podstawie wykładniki dodajemy: aᵐ · aⁿ = aᵐ⁺ⁿ. Z kolei przy dzieleniu potęg o tej samej podstawie, wykładniki odejmujemy: aᵐ : aⁿ = aᵐ⁻ⁿ.
Potęgowanie potęgi oznacza mnożenie wykładników: (aᵐ)ⁿ = aᵐⁿ. Dla liczb z wykładnikami ujemnymi stosujemy regułę: a⁻ⁿ = 1/aⁿ. Pamiętaj też, że a⁰ = 1 dla każdej liczby a różnej od zera.
Uwaga! Wyrażenie 0⁰ nie jest zdefiniowane w matematyce. Nigdy nie przypisujemy mu wartości!
Potęga o wykładniku wymiernym wiąże się z pierwiastkowaniem: a^m/n = ⁿ√aᵐ. Daje nam to możliwość zapisywania pierwiastków jako potęg o wykładnikach ułamkowych, co często upraszcza obliczenia.