Twierdzenie Talesa - podstawy i zastosowanie

Wyobraź sobie, że masz kąt, którego ramiona są przecięte przez dwie równoległe proste - to właśnie sytuacja, w której sprawdza się twierdzenie Talesa! Ta zasada mówi, że stosunek długości odcinków na jednym ramieniu kąta będzie zawsze równy stosunkowi odpowiednich odcinków na drugim ramieniu.

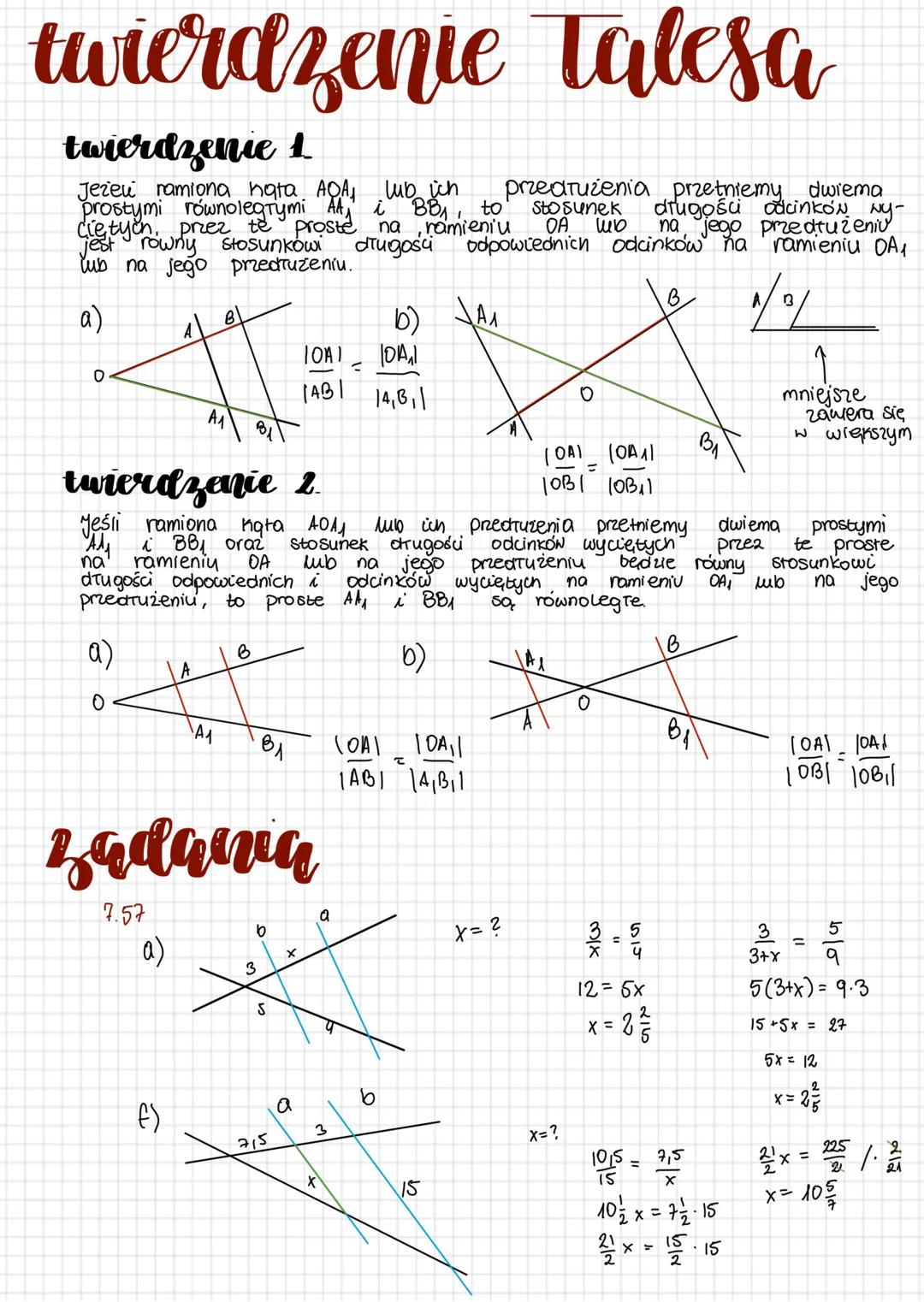
Twierdzenie 1 (podstawowe): Gdy dwie równoległe proste przecinają ramiona kąta, powstają proporcjonalne odcinki. Możesz to zapisać jako: $\frac{|OA|}{|AB|} = \frac{|OA_1|}{|A_1B_1|}$ lub $\frac{|OA|}{|OB|} = \frac{|OA_1|}{|OB_1|}$.

Twierdzenie 2 (odwrotne) działa w drugą stronę - jeśli stosunek odcinków jest równy, to znaczy, że proste są równoległe. To super przydatne, gdy chcesz udowodnić równoległość!

W praktycznych zadaniach, jak te z przykładu, używasz proporcji do znajdowania niewiadomej x. Na przykład: $\frac{3}{x} = \frac{5}{4}$, więc $5x = 12$, czyli $x = \frac{12}{5}$. Pamiętaj - zawsze mnożysz na krzyż i rozwiązujesz równanie!

💡 Wskazówka: Twierdzenie Talesa to twój klucz do rozwiązywania zadań z podobieństwem - wystarczy ułożyć proporcję i pomnożyć na krzyż!