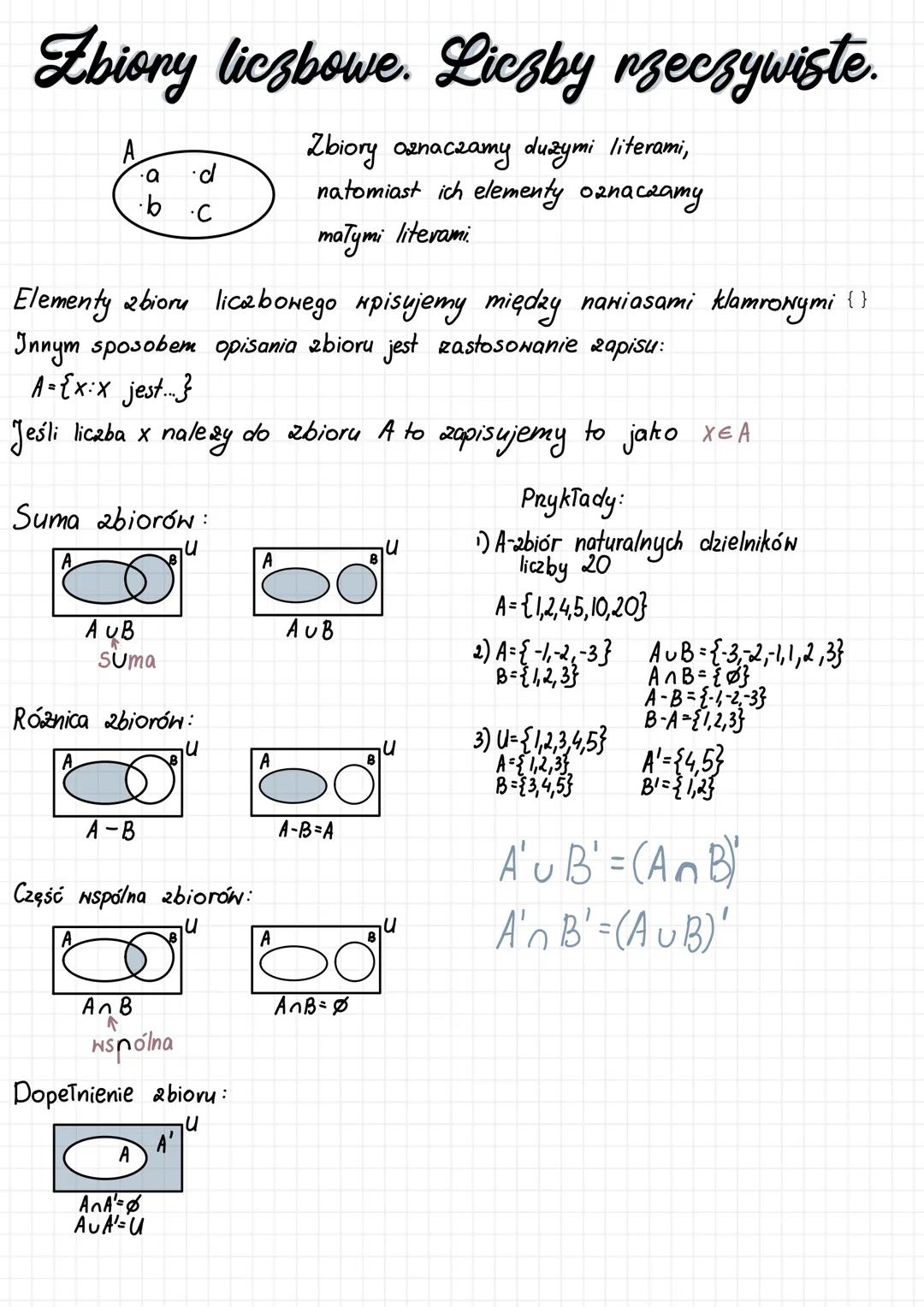
Zbiory liczbowe i liczby rzeczywiste

Zbiory to kolekcje obiektów, które oznaczamy dużymi literami, podczas gdy ich elementy zapisujemy małymi literami. Elementy zbioru umieszczamy w nawiasach klamrowych {}. Możemy też zapisać zbiór w formie: A={x:x jest...}, określając warunek przynależności.

Jeśli element x należy do zbioru A, zapisujemy to jako x ∈ A. Podstawowe operacje na zbiorach to: suma (A ∪ B), różnica $A - B$, część wspólna (A ∩ B) oraz dopełnienie zbioru (A'). Suma zbiorów zawiera wszystkie elementy należące do przynajmniej jednego z tych zbiorów. Różnica A - B zawiera elementy A, które nie należą do B.

Część wspólna zbiorów zawiera elementy należące jednocześnie do obu zbiorów. Jeśli A ∩ B = ∅, zbiory są rozłączne. Dopełnienie zbioru A oznaczamy A' i są to wszystkie elementy uniwersum U nie należące do A. Zawsze zachodzą zależności: A ∩ A' = ∅ oraz A ∪ A' = U.

⚠️ Uważaj! W zadaniach z dopełnieniem zbiorów zawsze musisz znać uniwersum U, czyli zbiór wszystkich rozważanych elementów. Bez określonego uniwersum nie da się poprawnie wyznaczyć dopełnienia.

Przykłady: Dla U={1,2,3,4,5}, A={1,2,3}, B={3,4,5} mamy: A ∪ B = {1,2,3,4,5}, A ∩ B = {3}, A' = {4,5}, B' = {1,2}. Zachodzi też ważna zależność: A' ∪ B' = (A ∩ B)' oraz A' ∩ B' = (A ∪ B)'.