Twierdzenie Pitagorasa i jego zastosowania
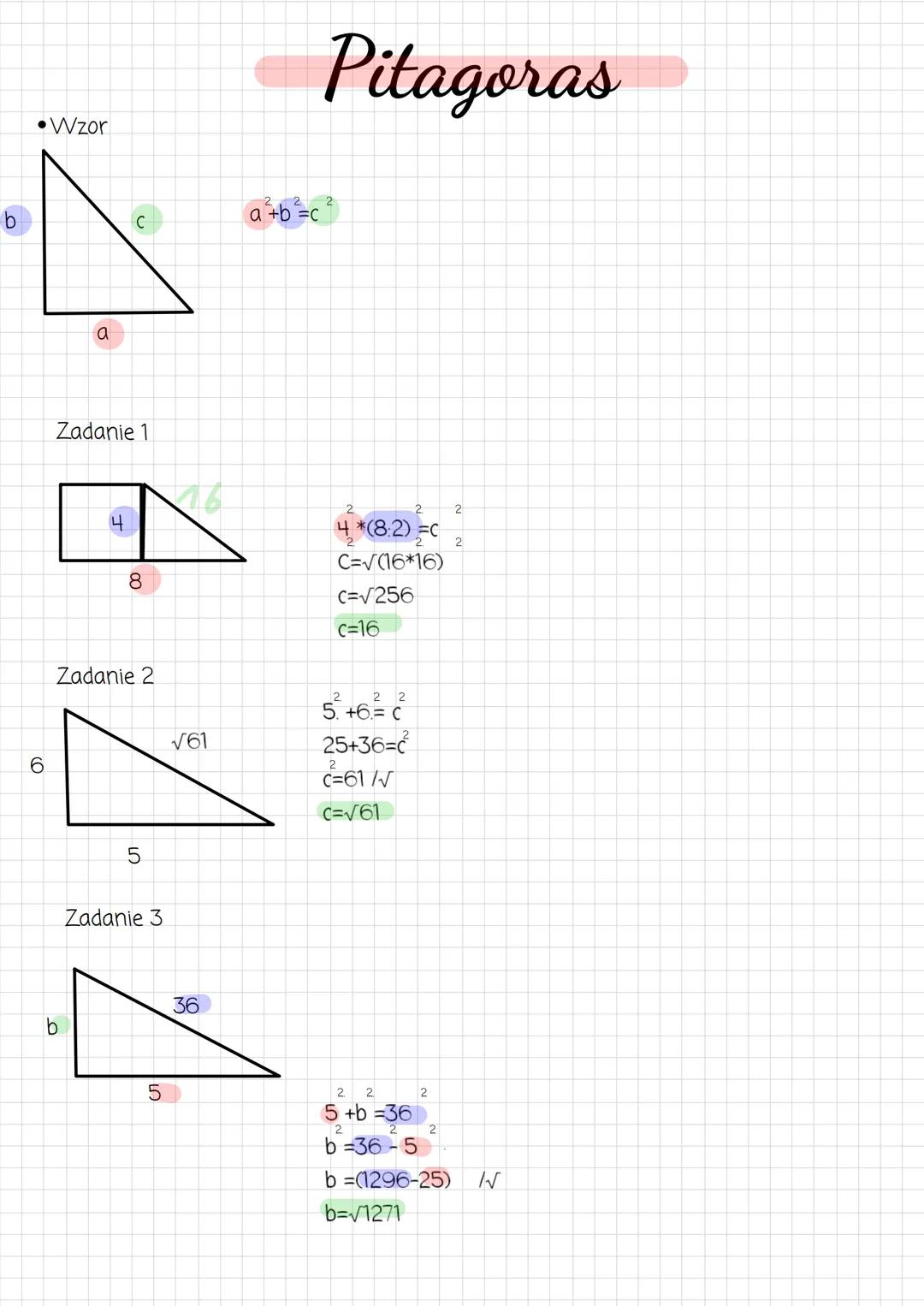
Twierdzenie Pitagorasa mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych (a i b) równa się kwadratowi długości przeciwprostokątnej (c). Zapisujemy to wzorem: a² + b² = c².
Na tej stronie mamy trzy zadania pokazujące, jak stosować twierdzenie Pitagorasa w praktyce. W pierwszym zadaniu, znając boki 4 i 8, obliczamy przeciwprostokątną: 4² + 8² = 16 + 64 = 80, więc c = √80 = √(16·5) = 4√5.
Wskazówka: Pamiętaj, że twierdzenie Pitagorasa działa tylko w trójkątach prostokątnych!
W drugim zadaniu obliczamy przeciwprostokątną trójkąta o bokach 5 i 6: 5² + 6² = 25 + 36 = 61, więc c = √61. W trzecim zadaniu szukamy boku b, gdy znamy przeciwprostokątną 36 i drugi bok 5: b² = 36² - 5² = 1296 - 25 = 1271, więc b = √1271.