Twierdzenie Pitagorasa - podstawy

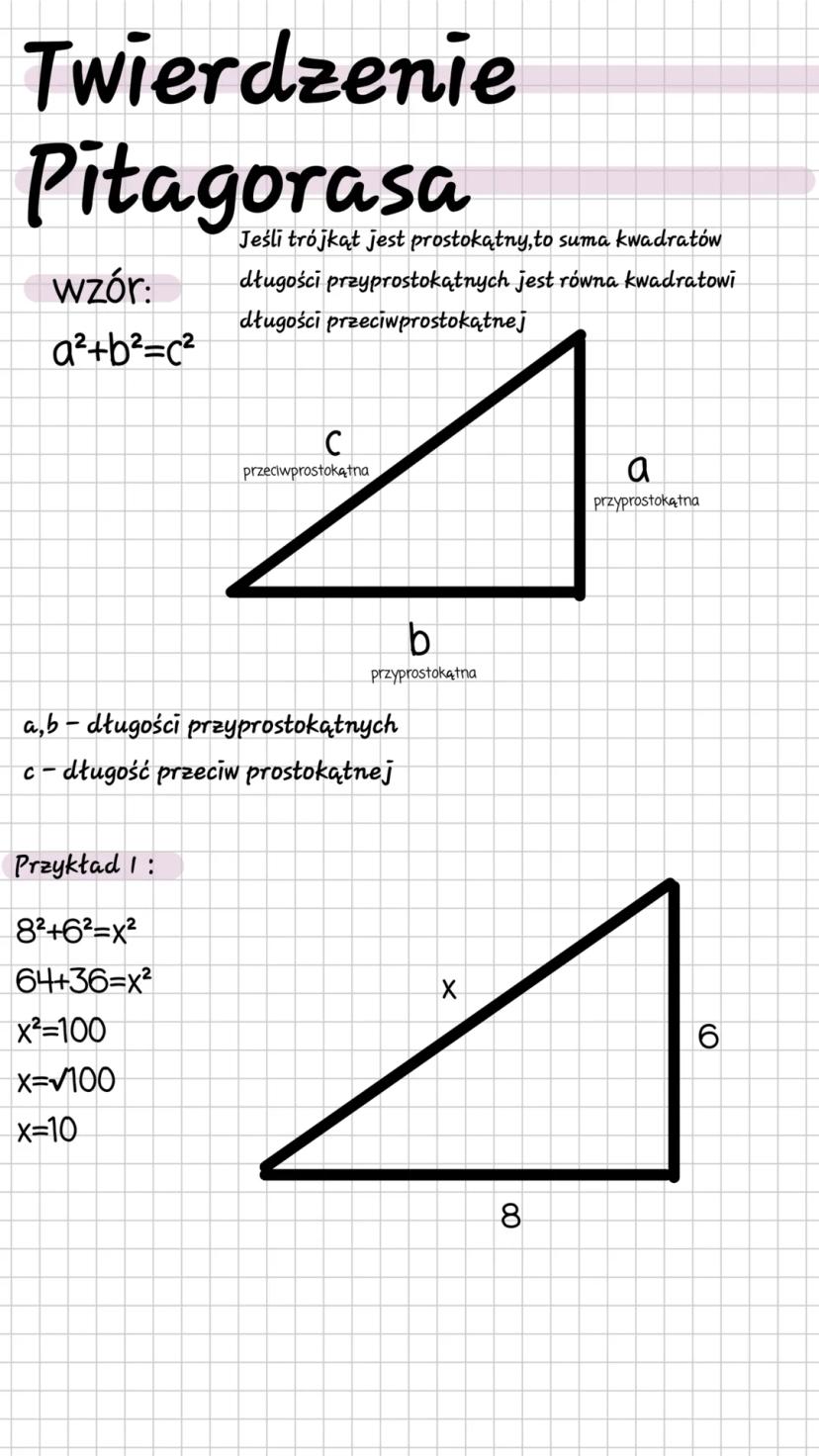
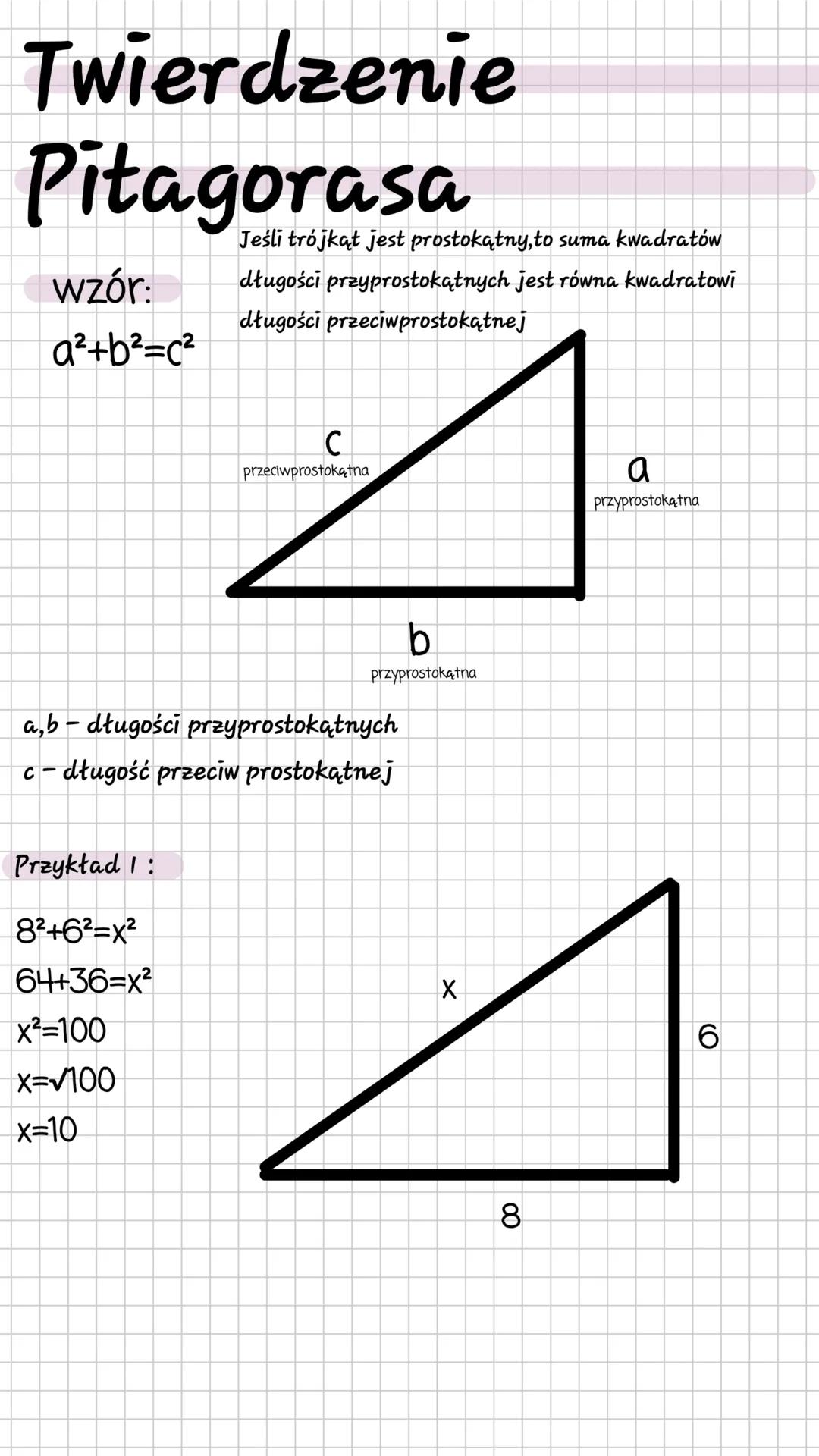
Twierdzenie Pitagorasa mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Zapisujemy to wzorem: a²+b²=c².

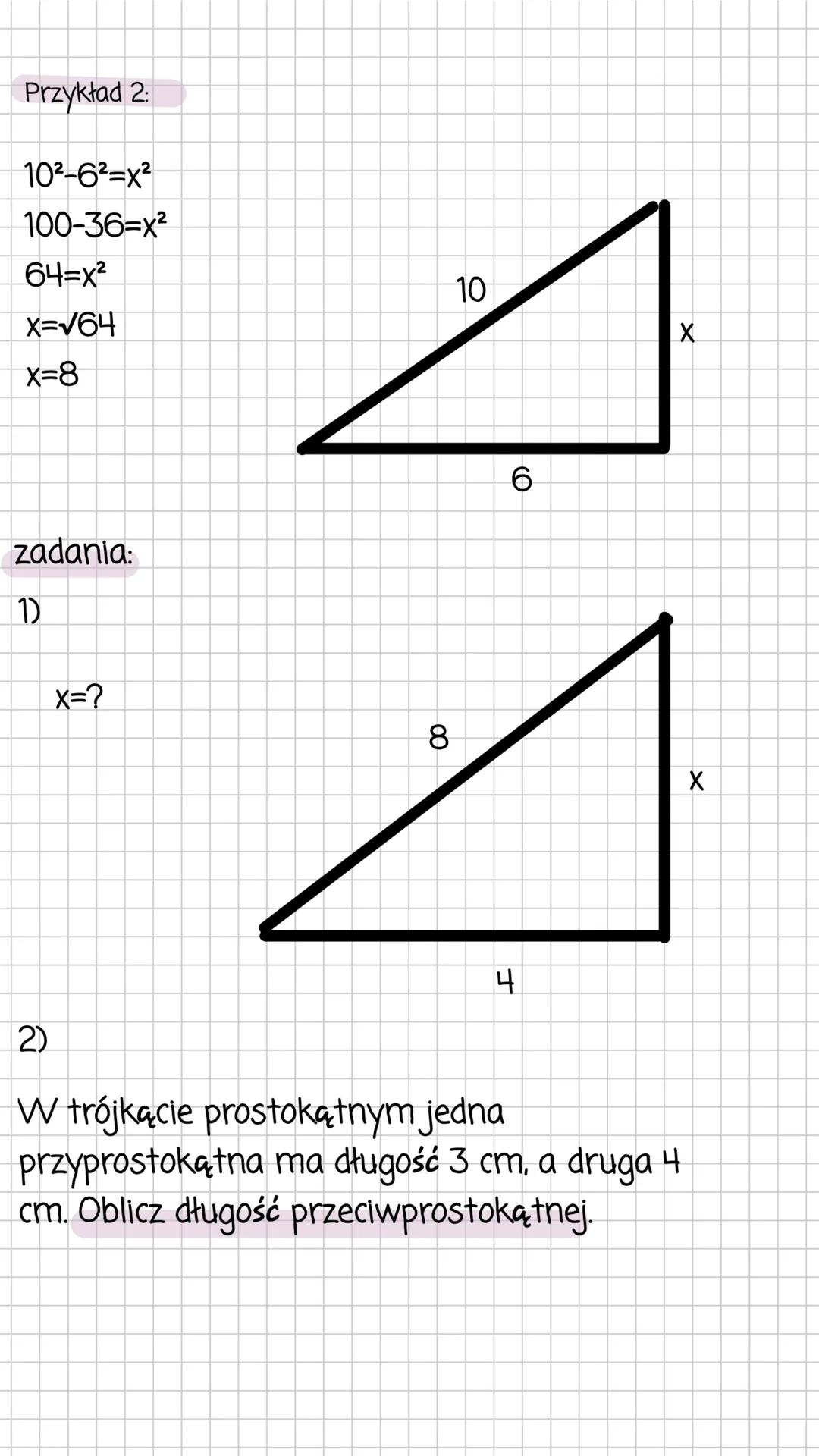
W trójkącie prostokątnym mamy dwie przyprostokątne (a, b) oraz przeciwprostokątną $c$. Przeciwprostokątna to najdłuższy bok, który leży naprzeciwko kąta prostego.

Zobaczmy to na przykładzie: Jeśli jedna przyprostokątna ma długość 8, a druga 6, to długość przeciwprostokątnej obliczamy tak: 8²+6²=x², czyli 64+36=100, zatem x=10.

💡 Pamiętaj! Twierdzenie Pitagorasa działa tylko w trójkątach prostokątnych, czyli takich, które mają jeden kąt równy 90°.

Zastosowanie twierdzenia Pitagorasa

Twierdzenie Pitagorasa możemy również wykorzystać do obliczenia długości przyprostokątnej, gdy znamy przeciwprostokątną i drugą przyprostokątną. W tym przypadku przekształcamy wzór: a² = c² - b².

Na przykład, jeśli przeciwprostokątna ma długość 10, a jedna z przyprostokątnych ma długość 6, to drugą przyprostokątną obliczamy: x² = 10² - 6² = 100 - 36 = 64, stąd x = 8.

Oto zadania do przećwiczenia:

1. Oblicz x, gdy przyprostokątne mają długości 8 i 4.
2. W trójkącie prostokątnym przyprostokątne mają długości 3 cm i 4 cm. Oblicz długość przeciwprostokątnej.

🔍 Wskazówka: Zawsze rysuj trójkąt i oznaczaj na nim dane - to znacznie ułatwia rozwiązywanie zadań!

Praktyczne zastosowania twierdzenia Pitagorasa

Twierdzenie Pitagorasa przydaje się w wielu różnych zadaniach. Możesz je wykorzystać do obliczania:

• długości przekątnej kwadratu (zadanie 3)
• wysokości trójkąta równoramiennego (zadanie 4)
• długości przeciwprostokątnej, gdy znasz przyprostokątne (zadanie 5)

Twierdzenie ma też zastosowania praktyczne, jak w zadaniu 6, gdzie obliczasz wysokość, na jakiej drabina opiera się o ścianę, czy w zadaniu 7, gdzie szukasz najkrótszej drogi po przekątnej prostokątnego placu.

👉 Twierdzenie Pitagorasa to nie tylko nudna teoria - używasz go w realnych sytuacjach, jak planowanie najkrótszej trasy czy projektowanie konstrukcji!

Rozwiązywanie zadań - przygotowanie

Zanim przejdziemy do rozwiązań, pamiętaj o kilku ważnych krokach, które pomogą Ci rozwiązać każde zadanie z twierdzeniem Pitagorasa:

1. Narysuj figure (trójkąt, kwadrat, itp.) i oznacz na niej wszystkie dane z zadania.
2. Zidentyfikuj, który bok jest przeciwprostokątną, a które przyprostokątnymi.
3. Podstaw dane do wzoru a²+b²=c² lub jego przekształcenia.

Świetnie sobie radzisz! Zadania z Pitagorasem mogą wyglądać trudno na pierwszy rzut oka, ale gdy poznasz wzór i przećwiczysz kilka przykładów, staną się dużo prostsze.

💪 Nie poddawaj się, jeśli pierwsze zadania wydają się trudne - z każdym kolejnym przykładem będzie łatwiej!

Rozwiązania zadań (część 1)

Zadanie 1: Używamy przekształconego wzoru Pitagorasa, bo szukamy przyprostokątnej. 8² - 4² = x² 64 - 16 = x² x² = 48 x = √48 ≈ 6,93

Zadanie 2: Klasyczne zastosowanie twierdzenia Pitagorasa. 3² + 4² = x² 9 + 16 = x² x² = 25 x = 5 cm

Zadanie 3: Obliczanie przekątnej kwadratu. 10² + 10² = x² 100 + 100 = x² x² = 200 x = 10√2 cm ≈ 14,14 cm

💡 W kwadracie możesz też użyć wzoru na przekątną: d = a√2, gdzie a to długość boku kwadratu!

Rozwiązania zadań (część 2)

Zadanie 4: Wysokość trójkąta równoramiennego. 10² - 6² = x² 100 - 36 = x² x² = 64 x = 8 cm

Zadanie 5: Przeciwprostokątna z wartością pierwiastkową. 10² + (√50)² = x² 100 + 50 = x² x² = 150 x = √150 cm ≈ 12,25 cm

Zadanie 6: Praktyczne zastosowanie - drabina. 5² - 3² = x² 25 - 9 = x² x² = 16 x = 4 m

Zadanie 7: Przekątna prostokątnego placu. 30² + 40² = x² 900 + 1600 = x² x² = 2500 x = 50 m

🏆 Świetnie! Teraz potrafisz stosować twierdzenie Pitagorasa w różnych sytuacjach - od prostych obliczeń po praktyczne zadania z życia codziennego!